«Квант» для «младших» школьников

Задачи первого номера 1971 года

1. На доске было произведено умножение двух чисел. Потом часть цифр стёрли и заменили звёздочками. Восстановите стёртые цифры.

2. На шахматной доске в нижнем левом углу стоит шашка. Два игрока ходят ею по очереди, передвигая шашку на соседнее поле. Допускаются лишь направления движений, указанные на рисунке. Выигрывает тот, кто своим ходом ставит шашку на верхнее правое поле. Как должен играть начинающий, чтобы выиграть?

3. При некоторой замене цифр буквами оказалось, что три + три + три = дыра, причём (ы + ы) : ы = ы. Каким цифрам соответствуют использованные в этих равенствах буквы? (Разным цифрам соответствуют разные буквы, одинаковым — одинаковые.)

Указание   Ответ

4. Обойдите фигуру, не отрывая карандаш от бумаги и не проходя дважды ни по какой линии.

Задачи третьего номера 1971 года

1. По дереву ползёт гусеница. За день она поднимается на 6 метров, а ночью опускается на 4 метра. За сколько дней она доползёт до вершины, если высота дерева — 14 метров?

2. Из 15 монет, одинаковых с виду, одна фальшивая. Неизвестно, тяжелее или легче она остальных. Научитесь это узнавать, сделав не более двух взвешиваний на чашечных весах без гирь.

3. Числа ***9 и 9*** являются кубами целых чисел. Каких?

4. Шесть спичек лежат на столе так, как показано на рисунке. Требуется поменять их местами, придерживаясь следующих правил: спичку можно перемещать лишь в направлении её головки на свободное место, либо просто передвигая, либо перепрыгивая не более чем через одну спичку.

5. Дан квадратный лист бумаги. Рассеките его прямыми на четыре части, чтобы из них можно было сложить треугольную пирамиду, все рёбра которой разной длины.

Задачи четвёртого номера 1971 года

1. За какое наименьшее число разломов можно полностью разломить шоколадку размером 4×8 на кусочки? Ломать можно только по прямым, являющимся углублениями на шоколадке. Ломать более одного куска одновременно нельзя.

2. Расшифруйте известное стихотворение:

Мяжя Дяма клёнгё брящэд,
Юлёмыря ф лэщгю нащыг.
Дыжэ, Дямэщгя, мэ брящъ,
Мэ юдёмэд ф лэщгэ нащ.

3. На рисунке изображены три верёвочных кольца. Если разрезать верхнее кольцо, то остальные окажутся свободными, если же разрезать одно из нижних, то оставшиеся останутся сцепленными. Зацепите три кольца так, чтобы при разрезании любого из них оставшиеся кольца оказались свободными.

4. Здесь крестиками зашифрованы некоторые цифры. Попробуйте расшифровать пример.

5. Равенство, изображённое на рисунке, неверно. Переложите одну спичку так, чтобы оно выполнялось с точностью до 0,01. (Подсказка. Посмотрите статью Н.М. Вескина «Цепные дроби» (первый номер «Кванта» 1970 года).)

Задачи седьмого номера 1971 года

1. На олимпийских играх спортсмены завоевали 96 медалей. Из них 65 золотых и бронзовых. А золотых и серебряных — 61. Сколько золотых, серебряных и бронзовых медалей получили они в отдельности?

Указание   Ответ  Решение

2. Мог ли некто разделить три яблока между некоторыми двумя отцами и двумя сыновьями так, что каждому досталось ровно по одному яблоку?

Указание   Ответ  Решение

3. На столе стоят в ряд три стакана пустых и три с молоком. Их нужно расположить так, чтобы пустые стаканы чередовались с наполненными. Для этого разрешено взять только один стакан. Как это сделать?

4. Нина живёт на четвёртом этаже, а Таня на втором. Нина поднимается на 60 ступенек. На сколько ступенек поднимается Таня?

5. В трёх ящиках лежит по одному шарику: белый, чёрный и зелёный. На первом ящике надпись «белый», на втором — «чёрный», а на третьем — «белый или зелёный». Ни одна надпись не соответствует действительности. Где что?

6. Вместо крестиков поставьте цифры в действии умножения.

7. Если Коля купит одну конфету, то у него останется одна копейка, а если он захочет купить 2 конфеты, то у него не хватит одной копейки. Сколько денег у Коли?

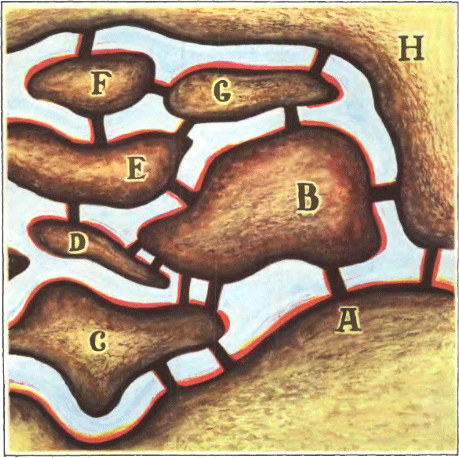8. Перёд нами план города. Можно ли составить маршрут прогулки так, чтобы пройти по каждому мосту только один раз?

Задачи восьмого номера 1971 года

1. Дана последовательность целых чисел, которая составлена по определённому математическому закону: 4, 7, 12, 21, 38, ... Продолжите ряд до восьмого числа.

2. Сумма уменьшаемого, вычитаемого и разности равна 624. Найдите уменьшаемое, вычитаемое и разность, если разность меньше вычитаемого на 56.

3. Найдите последние три цифры произведения всех натуральных чисел от 1 до 18.

4. Имеются два сосуда вместимостью в 3 л и 5 л. С помощью этих сосудов научитесь наливать из водопроводного крана 4 литра воды.

5. В таблицу вписаны числа по некоторому правилу:

2

3

5

9

33

а) Найдите это правило и впишите недостающие числа.

б) Аналогично — для следующей таблицы:

1

5

6

11

28

6. В магазине имеется мастика в ящиках по 16 кг, 17 кг и 21 кг. Отмерьте 185 кг мастики, не вскрывая ящики. (Найдите все варианты!)

7. На доске было произведено действие умножения. Потом часть цифр стёрли и заменили звёздочками. Восстановите стёртые цифры.

8. Ученик купил 4 книги. Все книги без первой стоят 42 коп., без второй — 40 коп., без третьей — 38 коп., без четвёртой — 36 коп. Сколько стоит каждая книга?

9. В каких случаях в месяце 5 понедельников?

10. На столе лежат 15 карандашей. Двое берут по очереди один, два или три карандаша. Проигрывает тот, кому осталось взять один последний карандаш. Как должен играть начинающий игру, чтобы заставить противника взять последний карандаш?

Задачи девятого номера 1971 года