«Квант» для «младших» школьников

Задачи первого номера 1972 года

1. Под окном у стены расположена батарея парового отопления. Трубы, по которым к батарее подводится горячая вода и отводится холодная, находятся слева. Справа в батарее имеются отверстия, закрытые с помощью ввинченных пробок. Сильный человек берётся завинтить эти пробки с помощью гаечного ключа. В каком случае он закрутит эти пробки сильнее: когда резьба на них правая или когда резьба левая? (Пробки завинчивают, плавно нажимая на ключ, а не ударяя по нему.)

2. Сколькими нулями оканчивается произведение всех чисел от 1 до 100?

3. Имеется пять электрических лампочек на 110 в мощностью 40, 40, 40, 60 и 60 вт. Как следует включить их в сеть с напряжением 220 в, чтобы все они горели полным накалом?

4. Пароход от Киева до Херсона идёт трое суток, а от Херсона до Киева четверо суток (без остановок). Сколько времени будут плыть плоты от Киева до Херсона?

5. Утка при ходьбе переваливается с боку на бок, а курица нет. Почему?

6. Почему зимой при резком потеплении на стенах кирпичных домов появляется иней? Почему иней редко появляется на стенах деревянных домов?

Задачи второго номера 1972 года

1. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость?

2. На рисунке изображена мишень. Куда надо попасть и сколько выстрелов сделать, чтобы выбить на ней ровно 100 очков?

3. Найдите цифры x и y пятизначного числа 42x4y, если оно делится на 72.

4. Каких чисел больше среди первого миллиона: тех, в записи которых встречается единица, или тех, в записи которых её нет?

5. Рассмотрим квадрат размером 5×5, в котором записаны 25 чисел:

4	0	8	12	2
7	3	11	15	5
10	6	14	18	8
13	9	17	21	11
16	12	20	24	14

Выберем одно из чисел (произвольно), закрасим его, а остальные числа, стоящие в том же столбце и в той же строке, зачеркнём. Затем выберем одно из оставшихся чисел, обведём его, а остальные числа в тех же строке и столбце зачеркнём. Так сделаем пять раз:

4	0	8	12	2
7	3	11	15	5
10	6	14	18	8
13	9	17	21	11
16	12	20	24	14

Возьмём сумму закрашенных чисел 0 + 15 + 14 + 13 + 14. Оказывается, как бы мы ни выбирали числа, эта сумма всегда равна 56. Попробуйте разгадать это таинственное свойство этого квадрата.

Задачи третьего номера 1972 года

1. Три подруги вышли в белом, зелёном и синем платьях. Их туфли были одного из тех же трёх цветов. Только у Ани цвета платья и туфель совпадали. Ни платье, ни туфли Вали не белые; Наташа была в зелёных туфлях. Определите цвет платья каждой из подруг.

2. Не развязывая верёвки, передвиньте кольцо из левой петли в правую.

3. У мальчика 25 медных монет. (Медные монеты в те годы чеканились следующих достоинств: 1, 2, 3 и 5 копеек.) Обязательно ли среди них есть семь монет одного достоинства?

4. Провода подключены к однородному металлическому шару в диаметрально противоположных его точках. В каком сечении шара выделяется при пропускании через шар электрического тока больше тепла?

5. В море на глубине нескольких километров затонула незакупоренная бутылка. Увеличилась или уменьшилась вместимость бутылки из-за давления воды?

6. Четыре одинаковых проводника заключены в трубу, соединяющую этажи здания. Провода выступают из трубы на нижнем и верхнем этажах на несколько сантиметров. Концы проводов на нижнем этаже перенумерованы. Как, совершив наименьшее число операций, узнать номера концов на верхнем этаже, имея в своем распоряжении батарейку, лампочку и короткий кусок провода?

Задачи четвёртого номера 1972 года

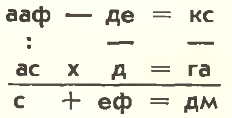1. Разгадайте числовой ребус, если каждая буква — это цифра.

2. Имеется шесть кнопок. Пока ни одна из них не нажата, лампочка не горит. При одновременном нажатии первой, второй и пятой кнопок лампочка загорается. Никакая другая комбинация нажатых кнопок лампочку не включает. Нарисуйте схему простейшей электрической цепи, обладающей такими свойствами.

3. Разместите числа 1, 2, 3, 4, 5, 6 по одному около вершин треугольника и около середин его сторон так, чтобы сумма трёх чисел, расположенных в концах и в середине любой стороны, была одна и та же.

4. Когда в жаркий день Вы входите в реку, вода кажется холоднее окружающего воздуха, а когда выходите — наоборот. Почему?

5. Впишите недостающие числа в таблицу:

10

8

11

9

12

10

13

?

?

6. Как можно определить плотность камня, если его объём измерить непосредственно невозможно?

Задачи пятого номера 1972 года

1. К стене прислонён обруч. В одной точке в стене «внутри» обруча вбит гвоздь так, что обруч касается его. Найти множество точек, в которые можно вбить второй гвоздь внутри обруча так, чтобы обруч оставался неподвижным.

2. В предлагаемой шифровке значками зашифрованы цифры и знаки +, –, ·, =. Каждая строчка шифровки содержит запись одного из арифметических действий типа 25 + 184 = 209 или 2568 = 2573 – 5. Определите, какой цифре или знаку соответствует каждый из значков.

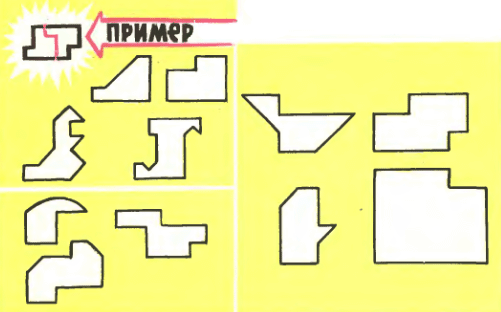3. Каждую из приведённых фигур разрежьте на две конгруэнтные фигуры, то есть на две такие фигуры, которые можно совместить, наложив одну на другую. В качестве примера на первой из этих фигур показан требуемый разрез.

Задачи шестого номера 1972 года

1. Впишите в пустые клетки таблицы недостающие числа:

7	10	13
22		30
4	9

2. Около каждой вершины треугольника поставьте какое-нибудь число. Напишите возле каждой стороны этого треугольника число, равное сумме чисел, стоящих у её концов. Теперь каждое число, стоящее около вершины, сложите с числом, стоящим около противоположной стороны. Почему равны все три полученные суммы?

3. Найдите нечётное четырёхзначное число, две средние цифры которого образуют число, в пять раз большее числа тысяч и в три раза большее числа единиц этого числа.

4. Может ли значение выражения ^{a + 9}/_{a + 6}, где a — целое, быть целым числом? Если да, то при каких целых значениях а?

5. В двух комнатах было 76 человек. Когда из одной комнаты вышло 30, а из второй 40 человек, то людей в комнатах осталось поровну. Сколько человек было в каждой комнате первоначально?

6. Представьте себе, что Вы машинист. Машинист ведёт поезд из Москвы во Владивосток. В составе 64 вагона: 14 вагонов с мебелью, 30 вагонов с бурым углём и 20 вагонов с солью. Делаете 3 остановки по 15 минут. До первой остановки поезд шёл со скоростью 60 км/ч. Сколько лет машинисту?

Задачи седьмого номера 1972 года

1. Разность 999 993¹⁹⁹⁹ — 555557¹⁹⁹⁷ кратна пяти. Докажите это.

2. Чтобы проверить горизонтальность поверхности, строители пользуются прибором, который называют плотничьим уровнем. В изогнутой трубке, заполненной водой, находится пузырёк воздуха. Если уровень лежит не горизонтально, пузырёк смещается к краю трубки. Когда пузырёк больше: в тёплую или в холодную погоду?

3. Выпишем подряд, начиная с 1, числа натурального ряда: 123456789101112131415161718192021... Какая цифра окажется на 1972-м месте?

4. Останкинская телебашня высотой 530 метров весит 30 000 тонн. Сколько весит точная модель этой башни высотой 53 см?

5. В погребе — 20 одинаковых банок с вареньем. В 8 банках клубничное варенье, в 7 — малиновое, в 5 — вишнёвое. Каково наибольшее число банок, которые можно в темноте вынести из погреба с уверенностью, что там осталось ещё хотя бы 4 банки одного сорта варенья и 3 банки другого?

6. Из всех прямоугольников одного и того же периметра наибольшую площадь имеет квадрат. Докажите это.

Задачи восьмого номера 1972 года

1. Команды «Динамо», «Спартак», «Труд» и «Шахтёр» сыграли каждая с каждой по одному матчу. Победа давала 2 очка, ничья — 1 очко. «Динамо» получило 5 очков, «Труд» — 3 очка, а «Шахтёр» — 1 очко. Было забито 11 голов, из которых 5 забили игроки «Труда». Эта команда победила «Шахтёр» со счётом 2 : 1. Восстановите исходы остальных матчей.

2. На рисунке города отмечены точками, соединяющие их дороги — отрезками (других дорог, кроме указанных на рисунке, нет). Найдите кратчайший путь от города А до города В при условии, что количество промежуточных городов чётно (таким образом, прямой путь от А к В не годится, ибо пролегает через нечётное количество городов).

3. Когда учитель вошёл в класс, дежурный стирал запись предыдущего урока, которую учитель собирался использовать. Остановив дежурного, учитель попросил его по оставшимся цифрам восстановить стёртые. Можно ли это сделать?

4. Два друга стояли внизу около эскалатора метро. Им хотелось сосчитать количество ступенек эскалатора, находящихся между входом и выходом с него. Однако вести счёт движущимся ступенькам оказалось не так просто, и вскоре друзья запутались. Тогда они решили применить более надёжный метод: одновременно ступили на эскалатор, причём в то время, как один делал два шага, другой делал один шаг (через ступеньки никто не перескакивал). Чтобы дойти до верхнего конца эскалатора, тому из друзей, который шагал быстрее, пришлось сделать 28 шагов, другой же сделал всего 21 шаг. Сколько ступенек в эскалаторе (снизу доверху)?

Задачи девятого номера 1972 года

1. Известному советскому математику А.Г. Постникову, находящемуся в расцвете творческих сил, в этом году исполняется m² + n² + p² лет. Родился он в (p⁴ + q⁴)-м году mn-го числа q-го месяца. Зная, что числа m, n, p, q образуют арифметическую прогрессию, установите дату рождения и возраст учёного.

2. Найдите наименьшее натуральное число, которое при умножении на 2 становится квадратом, а при умножении на 3 — кубом целого числа.

3. Расшифруйте равенство ** + *** = ****, если и сумма, и слагаемые — палиндромы: они одинаковы при чтении справа налево и слева направо.

4. Какое число надо вычесть из числителя дроби ⁵³⁷/₄₆₃ и прибавить к знаменателю, чтобы после сокращения получить дробь ¹/₉?

5. Найдите два таких числа, чтобы их сумма, произведение и частное от деления первого из них на второе были равны.

6. Брат говорит сестре: «Когда тёте Кате было столько лет, сколько теперь нам с тобой вместе, то тебе было столько лет, сколько мне сейчас. А когда тёте Кате было столько лет, сколько тебе сейчас, то тебе тогда было...» Сколько лет тогда было сестре?

7. Расшифруйте равенство: abcde · 4 = edcba, где abcde и edcba — не произведения, а пятизначные числа.

Задачи десятого номера 1972 года

1. На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, пришельцы всегда лгут. Путешественник нанял туземца-островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал проводника узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал, что тот говорит, что абориген. Кем был проводник: пришельцем или аборигеном?

2. Может ли конь попасть из левой нижней клетки шахматной доски в правую верхнюю, побывав при этом на каждой клетке один и только один раз?

3. Кончилась Великая Отечественная война (1941-1945). Как-то повстречались два товарища. Разговорились.
— Давненько мы с тобой не виделись. Сколько же теперь лет твоему сыну?— спросил один.
— Знаешь, любопытная игра чисел,— ответил второй. Сын мой родился в том самом году, который был точным квадратом ero возраста в год его рождения. Сейчас ему столько лет, какова сумма цифр года моего рождения. Сколько лет отцу-математику?

4. Из всех людей, живших когда-либо на свете и живущих сейчас, количество людей, сделавших в течение всей своей жизни нечётное число рукопожатий, есть число чётное. Докажите это.

5. abcd : dcda = q. Делимое, делитель и частное — точные квадраты. Найдите их. (Здесь abcd и dcda — не произведения, а четырёхзначные числа.)

Задачи одиннадцатого номера 1972 года

1. 9 одинаковых книг стоят 11 рублей с копейками, а 13 таких книг — 15 рублей с копейками. Сколько стоит одна книга?

2. У вас есть пружинные весы (динамометр), рассчитанные максимум на 200 н, а вам надо взвесить чемодан, который примерно в полтора раза тяжелее. Можете ли вы это сделать?

3. Я отпил треть стакана кофе и долил его молоком, потом я выпил четверть стакана и снова долил молоком, затем отпивал ¹/₅, ¹/₆ и ¹/₇ стакана, и каждый раз доливал его молоком. В другой раз я отпил ¹/₇ стакана кофе и долил его молоком, затем отпил ¹/₆ стакана и снова долил молоком, и так далее до ¹/₃ стакана. В какой раз я выпил больше кофе?

4. Почему чай или кофе остывают быстрее, если на них подуть?

5. Любую ли сумму из целого числа рублей, большего семи, можно уплатить без сдачи денежными билетами в 3 и 5 рублей?

6. В Средней Азии, где летом очень жарко, многие носят именно летом тёплые ватные халаты. Как вы думаете, жарче ли в таком халате, чем в лёгком платье?

Задачи двенадцатого номера 1972 года

1. По окончании кинофильма часть зрителей уехали в шести автобусах, причём во всех автобусах было поровну зрителей. Остальные зрители (их оказалось на 15 процентов больше) пошли пешком. Сколько зрителей было в кинотеатре, если зрительный зал вмещает не больше 400 человек, а в автобусах уехало больше 150 зрителей?

2. Найдите все возможные способы расставить вместо звёздочек цифры в следующем равенстве *00** = (***)² (ни одно число не должно начинаться с нуля).

3. В трёх кучках находится 22, 14 и 12 орехов. Требуется путем трёх перекладываний уравнять число орехов в каждой кучке, соблюдая при этом условие: из любой кучки разрешено перекладывать в другую лишь столько орехов, сколько их в этой второй кучке имеется.

4. a и c — цифры. Расшифруйте равенство

5. Сложите из шести спичек четыре одинаковых равносторонних треугольника.

6. У треугольника, длины сторон которого — целые числа, длина одной стороны равна 5, а другой — 1. Чему равна длина третьей стороны?