«Квант» для «младших» школьников

Задачи первого номера 1983 года

1. Пошёл было Иван-царевич куда глаза глядят искать Василису Прекрасную, похищенную Кащеем, как навстречу ему Леший. «Знаю,— говорит,— я дорогу в Кащеево царство, случалось, ходил туда. Шёл я четыре дня и четыре ночи. Первые день и ночь — прямой дорогой на север, и прошёл я треть пути. Потом повернул на запад, продирался лесом сутки — прошёл вдвое меньше. И третьи сутки шёл лесом, уже на юг, и вышел на прямую дорогу, ведущую на восток. Прошагал я по ней за сутки сто вёрст и попал в Кащеево царство. Ты ходок такой же резвый, как и я: иди, Иван-царевич, глядишь, на пятый день будешь в гостях у Кащея». «Нет,— ответил Иван-царевич,— если всё так, как ты говоришь, то уже завтра я увижу Василису Прекрасную». Прав ли он? Сколько вёрст прошёл Леший и сколько думает пройти Иван-царевич?

2. Задумано трёхзначное число, у которого с любым из чисел 543, 142 и 562 совпадает один из разрядов, а два других не совпадают. Какое число задумано?

3. В этом числовом ребусе почти ничего неизвестно, однако он допускает лишь одно решение. Найдите его.

4. Шарик для игры в пинг-понг подбросили вверх. Что займёт больше времени — подъём или спуск?

Задачи второго номера 1983 года

1. Угадайте закономерность форм фигурок. Какую фигуру следует поставить следующей?

2. Отношение двух чисел равно десятичной дроби, целая часть которой равна делителю, а после запятой записан делитель. Какие это числа?

3. Вертушку погрузили целиком в ручей так, что её ось расположилась горизонтально и перпендикулярно направлению течения. Будет ли она крутиться?

4. Расшифруйте следующий вопрос и ответьте на него:

5343934*150413*6*8156215044414**305041080?

Текст зашифрован с помощью таблицы: каждой цифра обозначает одну из трёх букв, расположенных под ней в таблице, а знак «*» — пробел или одну из букв «ю», «я».

Задачи третьего номера 1983 года

1. Лёня и Коля пошли в гости к Боре, но забыли номер его квартиры. Коля помнил, что если прибавить к этому номеру 10, то получится точный куб, а Лёня помнил, что если вычесть из номера квартиры число 10, то получится точный квадрат. В какой квартире живёт Боря?

2. Маше нужны были для шитья нитки № 20. У неё не было таких ниток, но были нитки № 40 и № 10. Может ли она что-то сделать? (Номер нитки определяется как отношение длины нитки в метрах к её массе в граммах, то есть он численно равен длине в метрах 1 грамма ниток.)

3. Надутый воздухом воздушный шарик взвесили на весах. Потом надули его ещё сильнее и вновь взвесили. Одинаковы ли будут показания весов?

4. Какое число нужно поставить вместо звёздочки в последовательность 10, 11, 12, 13, 14, 15, 16, 17, 20, 22, 24, 31, 100, *, 10 000?

5. Вершина A треугольника ABC соединена отрезком с точкой M на противоположной стороне треугольника. Вершина B соединена с точкой K противоположной вершине B стороны треугольника. Могут ли отрезки AM и BK, пересекаясь, делиться пополам?

Задачи четвёртого номера 1983 года

1. Мой знакомый Саша однажды мне сказал: «Позавчера мне было 10 лет, а в будущем году мне исполнится 13 лет». Могло ли так быть?

2. Две высоты треугольника не меньше сторон, на которые они опущены. Найти величины углов треугольника.

3. Сломаем пополам спичку. Одну половинку переломим ещё раз. Один из получившихся кусочков снова попытаемся переломить пополам. Почему с каждым разом ломать спичку становится все труднее?

4. Найдите все пятизначные числа, равные кубу числа, образованного двумя их последними цифрами.

5. Какое число нужно поставить вместо звёздочки в последовательности 17, 23, 13, 11, *, 15?

Задачи пятого номера 1983 года

1. За книгу заплатили рубль, и осталось заплатить ещё столько, сколько осталось бы заплатить, если бы за неё заплатили столько, сколько осталось заплатить. Сколько стоит книга?

2. Расставьте в кружочках на рисунке числа 1, 2, 3, 4, 5, 6, 7 так, чтобы суммы пяти троек чисел, расположенных по «отрезкам», были равны между собой.

3. Найдите наибольшее число, на которое делится произведение любых трёх последовательных чётных чисел.

4. Двое играют в «крестики-нолики» на доске 3×3 по изменённым правилам: каждый на своём ходу может поставить как «крестик», так и «нолик». Выигрывает тот, после хода которого образуются три подряд стоящих одинаковых значка (по вертикали, горизонтали или диагонали — как в обычных «крестиках-ноликах»). Кто выигрывает при правильной игре — начинающий или второй игрок? И как?

5. В солнечный день я ехал на машине по мокрой дороге с дядей Серёжей, опытным водителем. Комочки грязи, летящие из-под колес впереди идущих машин, попадали на лобовое стекло. Когда машина остановилась по красному сигналу светофора, я спросил:
— Дядя Серёжа, можно я быстренько вытру стекло мокрой тряпкой?
— Ни в коем случае,— ответил дядя Сережа,— иначе придётся это делать постоянно!
Объясните, в чём тут дело.

Задачи шестого номера 1983 года

1. Восемь косточек домино лежат на столе так, как показано на рисунке. Какое значение имеет закрытая часть косточки домино, если эти косточки можно расположить в «магический квадрат» 4×4 (то есть так, чтобы сумма очков на косточках в каждом вертикальном ряду, в каждом горизонтальном ряду и по каждой диагонали была одинаковой)? Добейтесь такого расположения.

2. Братья Алёша и Боря родились в августе. В школе начинают учиться с семи лет. Номер класса, в котором учится сейчас старший брат Борис, равен возрасту Алёши. В какой класс перейдёт Алеша, когда Борис окончит среднюю школу?

3. На прямой расположили несколько точек. Затем между каждыми двумя соседними точками поставили ещё по точке. И так несколько раз. Докажите, что после каждой такой операции общее количество точек будет нечётным.

4. Дорога от дома до школы занимает у Пети 20 минут. Однажды он по дороге в школу вспомнил, что забыл дома ручку. Петя знал, что если он продолжит путь в школу с той же скоростью, то придёт туда за 8 минут до звонка, а если вернётся домой за ручкой, то, двигаясь с той же скоростью, опоздает к началу урока на 10 минут. Какую часть пути он прошёл?

5. Направление вращения Земли вокруг своей оси совпадает с направлением обращения Земли по орбите вокруг Солнца. На сколько изменилась бы продолжительность земных суток, если бы Земля вращалась вокруг своей оси с той же угловой скоростью в противоположном направлении?

Задачи седьмого номера 1983 года

1. В люстре 5 лампочек. Переключатель имеет 6 положений, при которых каждый раз горит разное количество лампочек — от 0 до 5. Однажды несколько лампочек перегорело. Какое наименьшее число раз нужно переключить переключатель, чтобы узнать, какие именно?

2. Найдите все трёхзначные числа, которые равны произведению числа, записываемого его двумя последними цифрами, на число, выражаемое его последней цифрой.

3. В клетках квадрата 3×3 расставили числа 1, 2, ..., 8, 9. Затем в каждом кружке записали среднее арифметическое окружающих его четырёх чисел. После этого вычислили среднее арифметическое полученных четырёх чисел. Какое наибольшее число могло получиться?

4. В бочке 18 литров бензина. Имеются два ведра объёмом по 7 литров, в которые нужно налить по 6 литров бензина. Кроме того, есть черпак объёмом 4 литра. Cможете осуществить розлив?

5. Почему днём из комнаты, окно которой завешено тюлевой занавеской, предметы на улице хорошо различимы, а предметы, находящиеся в комнате, с улицы не видны?

Задачи восьмого номера 1983 года

1. Расшифруйте ребус

ОДИН + ОДИН = МНОГО.

Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

2. Возьмите шестизначное число, которое делится хотя бы на одно из чисел из списка: 7, 13, 11, 37. Переставьте первую цифру в конец числа. Проверьте, что полученное число вновь будет иметь тот же делитель из списка, что и первоначальное. Почему?

3. Из восьми фигурок, сделанных из правильных треугольников, составьте один большой правильный треугольник.

4. В моей квартире две комнаты. Число, выражающее площадь первой комнаты в квадратных метрах, на единицу больше числа, выражающего периметр этой комнаты в метрах, а площадь второй комнаты в квадратных метрах, на единицу меньше её периметра. Каковы размеры этих комнат, если и длина, и ширина любой из двух комнат выражаются целыми числами метров?

5. Сидя в кресле зубного врача, пациент заметил, что вместе с другими инструментами врач прогрел и зеркальце. «Вы кладёте зеркало в горячую воду для стерилизации?»— спросил пациент. «Не только для этого»— ответил врач. А для чего ещё?

Задачи девятого номера 1983 года

1. Гена вырезал из бумаги десять карточек и на каждой из них написал по цифре: 0, 1, 2, ..., 8, 9. Затем он разложил их на столе по две и обнаружил, что полученные двузначные числа относятся как 1 : 2 : 3 : 4 : 5. Вечером он захотел показать свой результат отцу, но не нашёл карточку с цифрой 0. Однако, подумав, он разложил карточки так, что новые числа также относились, как 1 : 2 : 3 : 4 : 5. А вы так можете?

2. На ежегодном «конкурсе тыкв», проводимом в Великобритании, очередная «чемпионка» была массой 109 килограммов и 2,5 метра в обхвате. Могла ли она плавать в воде? Мог ли на ней, как на плоту, плавать мальчик, если его масса 20 килограммов? При расчётах считайте тыкву шаром, объём шара радиуса R равен 4πR³/3.

3. В обычном наборе домино 28 косточек. Сколько косточек содержало бы домино, у которого значения, указанные на косточках, изменялись бы не от 0 до 6, а от 0 до 12?

4. Отрезок AD — биссектриса треугольника ABC. Сравните величины углов ADB и ADC, если отрезок AB длиннее отрезка AC.

5. Коля сделал доску (для игры, называемой «йога») и раскрасил её на манер шахматной, как показано на рисунке. Как-то раз он решил обойти все поля этой доски одной шашкой, побывав на каждом поле по одному разу и переходя с поля на поле через сторону соответствующего квадратика. Он заметил, что если он начинает с белого поля, то такой обход ему удаётся, а если с рыжего поля — то не удаётся. Почему?

Задачи десятого номера 1983 года

1. Симметричен ли узор рисунка?

Ответ   Комментарий

Ответ. Нет.

Комментарий. Перевернув одну из звёздочек, получим симметричную фигуру:

2. Имеется два шарика красного цвета, два — синего, два — зелёного, два — жёлтого и два — белого. На одну чашку весов положили несколько разноцветных шариков, а на другую — вторые шарики этих цветов. При этом перевесила левая чашка весов. Однако было замечено, что какую бы пару шариков одного цвета ни поменять местами, весы либо окажутся в равновесии, либо перетянет правая чашка. При каком количестве шариков на весах это может быть?

Ответ   Указание   Решение

Ответ. Один или два шарика на каждой из чаш.

Указание. Докажите, что каждый шарик левой чаши тяжелее, чем шарик того же цвета правой чаши.

Решение. Во-первых, каждый шарик левой чаши тяжелее, чем шарик того же цвета правой чаши (если бы было не так, то нашлась бы пара шариков таких, что шарик на левой чаше не тяжелее шарика того же цвета на правой чаше; поменяв их местами, мы не нарушили бы положения весов).

Если количество шариков на каждой чаше не меньше трёх, то, поменяв местами ту пару шариков, у которой разность масс наименьшая, мы не изменим положения весов. Следовательно, шариков на чашах не более, чем по два. Может, очевидно, лежать и по одному шарику. Если же лежит по два шарика, нужно, чтобы разность масс у каждой пары одноцветных шариков была одинакова.

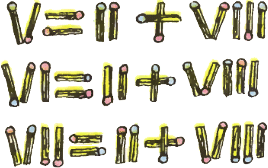3. Переставьте в каждом из неверных равенств V = II + VIII, VI = II + VIII и VII = II + VIII по одной спичке так, чтобы везде получились верные равенства.

4. Квадрат разрезан на прямоугольники так, что никакая точка квадрата не является вершиной сразу четырёх прямоугольников. Докажите, что количество точек квадрата, являющихся вершинами прямоугольников, чётно.

5. Стальной шарик плавает в ртути. Увеличится или уменьшится глубина погружения, если повысится температура?

Ответ   Решение

Ответ. Шарик опустится.

Решение. При нагревании ртуть расширяется сильнее, чем сталь, поэтому выталкивающая сила уменьшится, шарик опустится.

Задачи одиннадцатого номера 1983 года

1. Журнал «Квант» состоит из 16 вложенных друг в друга двойных листов. На каком двойном листе сумма чисел, обозначающих номера страниц, наибольшая?

2. Найдите двузначное число, вдвое большее произведения его цифр.

3. Решите пять «географических» ребусов: И^Н = ДИЯ, ЯП^О = НИЯ, АНГ = ОЛ^А, СЕ^Н = ЕГАЛ и МЕКС = ИК^А.

В каждом ребусе одинаковым буквам соответствуют одинаковые цифры, а разным — разные.

4. Кости домино выложены в виде кружевной салфетки, причём сумма очков в каждом вертикальном и в каждом горизонтальном ряду одна и та же. Значения очков на костях, кроме «пустышек», зашифрованы буквами. Расшифруйте их.

5. Отец и сын наблюдали солнечное затмение, и темой их разговоров были Солнце и Луна. «Папа,— спросил мальчик,— а во сколько раз Солнце дальше от нас, чем Луна? «Насколько я помню,— отвечал отец,— в 387 раз». «Тогда я могу подсчитать, во сколько раз объём Солнца больше объёма Луны». «Пожалуй, ты прав»,— ответил, подумав, отец. Во сколько же раз объём Солнца больше объёма Луны?

Задачи двенадцатого номера 1983 года

1. Возьмём два двузначных числа и перемножим их. Пусть a — их произведение. Теперь в каждом сомножителе переставим цифры и полученные числа также перемножим; получим число b. Докажите, что разность a – b делится на 99.

2. Докажите, что на рисунке закрашена ровно половина площади правильной пятиконечной звезды.

Указание   Ответ

Указание. Разрежьте закрашенную часть пятиугольника на части, из которых можно сложить незакрашенную часть пятиугольника.

Ответ.

3. Два гроссмейстера возвращались в гостиницу после очередного тура ежегодного шахматного турнира.
— Три восьмых турнира позади,— сказал один.
— Да,— ответил другой.— А участников с каждым годом делается всё больше. Подумай только, уже сыграно столько партий, сколько в прошлом году было сыграно за весь турнир!
— Если дело так пойдёт дальше,— усмехнулся первый,— то через несколько лет в турнире будет уже играть человек 30...
Сколько шахматистов играло в турнире?

4. Существует ли фигура на плоскости, не имеющая ни оси симметрии, ни центра симметрии, но переходящая в себя после поворота вокруг некоторой точки на угол, меньший 360°?

Указание   Ответ

Указание. Нарисуйте «вертушку».

Ответ.

5. В ребусах на рисунке каждому цвету соответствует число. Однако некоторые цветные кружки закрыты чёрными масками. Найдите числа, соответствующие каждому из цветов, и цвета кружков под масками. (В этом ребусе, кроме правил сложения чисел, выполняются ещё правила сложения цветов.)