2. Решите ребус
ШЕПНУЛ + ШЕПНУЛ + ШЕПНУЛ + ШЕПНУЛ + ШЕПНУЛ = КРИКНУЛ.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
Указание
Ответ
Указание. Очевидно, К = 1 и Л = 0 или 5.
Ответ. ШЕПНУЛ = 628750 или 682750.
3. Однажды я заблудился в лесу. Уже собирался остановиться, чтобы развести костер и заночевать, как споткнулся о водопроводную трубу. Ясно, что нужно идти вдоль трубы, но в какую сторону? Туда, куда течёт вода, ведь она течёт к людям. А как определить, куда течёт вода?
Указание
Ответ
Указание. Можно разжечь костёр.
Ответ. Можно разжечь костёр рядом с трубой и проследить, с какой стороны труба будет сильнее нагреваться. В ту сторону и течёт вода.
4. Урожай фруктов в этом году был отличный. Мы наварили 19 банок варенья. Я расставил их на трёх полках в погребе так, чтобы на каждой полке стояло одинаковое количество литров варенья. На первую полку я поставил одну большую и четыре средние банки, на вторую — две большие и шесть литровых банок, а на третью — одну большую, три средних и три литровых банки. Сколько литров варенья мы сварили?
Ответ
Решение
Ответ. 54.
Решение. Из сравнения первой и третьей полок следует, что объём средней банки равен 3 литрам. Сравнив вторую и третью полки, замечаем, что на третьей полке стоит половина того, что стоит на второй полке, и ещё три средних банки. Таким образом, половина объёма варенья на полке умещается в трёх средних банках, что составляет 9 литров. Значит, на одной полке стоит 18 литров, а на всех трёх полках — 54 литра варенья.
5. Два джентльмена были чрезвычайно схожи в своих привычках и (видимо, поэтому) терпеть друг друга не могли. Однажды, прогуливаясь по улице, они увидели друг друга и одновременно свернули в парк: один в ворота A, второй — в ворота B. Каждый решил обойти этот хорошо знакомый им парк, пройдя ровно по одному разу по каждой дорожке. Докажите, что если они всё время будут двигаться с одинаковыми скоростями, то непременно встретятся.
Указание
Решение
Указание. Каждый из джентльменов выходит из парка в той же точке, в которой входит.
Рассмотрите четыре случая: когда один джентльмен входит по дорожке AC, а другой входит по дорожке BC; когда один джентльмен входит по дорожке AC, а другой входит по дорожке BE; когда один джентльмен входит по дорожке AD, а другой входит по дорожке BE; наконец, когда один джентльмен входит по дорожке AD, а другой входит по дорожке BC.
Решение. Будем считать, что сторону квадрата каждый джентльмен проходит за одну минуту.
Если первый джентльмен входит в парк по дорожке AD, то выходит из парка по дорожке CA, и наоборот; аналогично, если второй джентльмен входит в парк по дорожке BE, то выходит по дорожке CB, и наоборот. Если первый джентльмен пошёл по AC, а второй по BC, то через 2 минуты они встретятся в точке C. Если первый джентльмен пошёл по AD, а второй по BC, то второй обязан идти к точке D (поскольку в противном случае он не сможет туда попасть, не проходя дважды по одной дорожке), и джентльмены встречаются в точке D через 5 минут после входа в парк.
Маршруты, начинающиеся с AD и BE, обратны маршрутам первого случая, и джентльмены встречаются в точке C за 2 минуты до выхода из парка, а маршруты, начинающиеся с AC и BE, обратны маршрутам второго случая, и встреча произойдёт за 5 минут до выхода джентльменов из парка.
Задачи второго номера 1987 года
1. У меня дома есть три ведра, каждое из которых вмещает целое число литров. Если вылить полное первое ведро воды во второе, то вода займёт 2/3 его объёма, а если вылить полное первое ведро в третье, то вода займёт 3/4 его объёма. Однажды я наполнял водой тридцатилитровую бочку, сначала вылив первое ведро, потом второе, затем третье ведро, но бочка ещё не наполнилась. Сколько литров воды можно ещё в неё влить?
Ответ
Решение
Ответ. 7.
Решение. Обозначим объёмы ведер через a, b и c. По условию, a = 2b/3 и a = Зс/4. Так как числа a, b и c целые, то a делится на 2 и на 3, то есть делится на 6. Если a = 6, то b = 9, c = 8 и a + b + c = 23, следовательно, в бочку можно долить 30 – 23 = 7 литров воды. Если a > 6, то a ≥ 12, b ≥ 18 и c ≥ 16, откуда a + b + c ≥ 46, что противоречит условию задачи.
2. Решите арифметический ребус, изображённый на рисунке. Разным буквам соответствуют разные цифры, одинаковым — одинаковые.
Ответ
Ответ. ПЯТЬ = 6284 или 6824.
3. В Великобритании и США температуру принято измерять по шкале Фаренгейта, по которой температура плавления льда составляет 32°, а температура кипения воды 212°. Укажите температуру, при которой количества градусов по шкалам Цельсия и Фаренгейта совпадают.
Ответ
Решение
Ответ. –40°.
Решение. Так как обе шкалы равномерные, мы можем написать связь между температурами по Фаренгейту F и по Цельсию C в виде F = aC + b. Подставляя C = 0, находим b = 32; а при C = 100 получаем 212 = 100a + 32, откуда a = 1,8. Теперь из уравнения C = 1,8C + 32 получаем, что при C = –40° Цельсия температура по Фаренгейту тоже равна –40°.
4. Шеф секретной службы составил следующую инструкцию взаимной слежки для своих семи главных агентов: агент 001 следит за тем, кто следит за агентом 002, агент 002 — за тем, кто следит за агентом 003, и так далее; агент 007 следит за тем, кто следит за агентом 001. Но вдруг пришёл приказ — взять на службу ещё агента 008. Сможет ли шеф составить аналогичную инструкцию для восьми агентов?
Ответ
Указание
Ответ. Нет.
Указание. Расставьте агентов по кругу так, чтобы рядом по часовой стрелке от каждого агента стоял тот, за которым он следит.
5. Имеется куб и шесть одинаковых крестообразных фигур, вырезанных из бумаги. Площадь каждой бумажной фигуры равна площади одной грани кубика. Можно ли этими кусками бумаги целиком оклеить поверхность куба?
Ответ
Указание
Решение
Ответ. Да, можно.
Указание. На каждую грань куба наклейте по одной фигуре и загните уголки.
Решение. На каждую грань куба наклейте по одной фигуре, как показано на левом рисунке, и загните уголки, как на правом.
Задачи третьего номера 1987 года
1. Имеются два пластмассовых кубика одного размера. Первый плавает в воде, опускаясь в воду на 2 см, а второй — на 1 см. На сколько опустится в воду нижний кубик, если первый кубик поставить на второй? А если второй на первый?
Ответ
Ответ. В обоих случаях кубик опустится на 3 см.
2. Мадемуазель Дюбуа любит домашних животных. Все её животные, кроме двух,— собаки, все, кроме двух,— кошки, и все, кроме двух,— попугаи; остальные — тараканы. Сколько каких животных у мадемуазель Дюбуа?
Ответ
Ответ. Либо животных меньше трёх, либо это собака, кошка и попугай.
3. Два конгруэнтных бумажных выпуклых четырёхугольника разрезали: первый — по одной из диагоналей, а второй — по другой диагонали. Сложите из полученных частей параллелограмм.
Решение
Решение. Сложим из четырёх полученных треугольников четырёхугольник, как показано на рисунке.
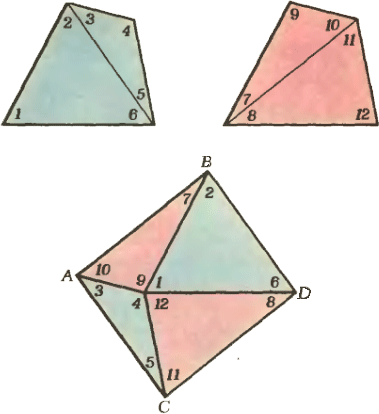
Это можно сделать в силу равенства соответствующих сторон треугольников и того факта, что сумма углов 1, 4, 9 и 12 равна 360° (как сумма внутренних углов четырёхугольника). Параллельность сторон полученного четырёхугольника нетрудно проверить: поскольку сумма углов 10 и 11 равна углу 1, то сумма углов 10, 3, 5, 11 равна 180°, следовательно, стороны AB и CD параллельны; параллельность сторон AC и BD доказывается аналогично.
4. «Медные» монеты достоинством 1, 2, 3 и 5 копеек весят соответственно 1, 2, 3 и 5 граммов. Среди четырёх «медных» монет (по одной каждого достоинства) одна — бракованная: отличается весом от нормальной. Научитесь с помощью взвешиваний на чашечных весах без гирь определять бракованную монету.
Указание
Решение
Указание. Положите на левую чашку монету в 5 коп., а на правую чашку монеты 2 и 3 коп.
Решение. Положим на левую чашку монету в 5 коп., а на правую чашку монеты 2 и 3 коп. Если весы в равновесии, то бракованная монета — 1 коп. Если перевесит одна из чашек, то положим на левую чашку монету 3 коп., а на правую — 2 и 1 коп. Если весы окажутся в равновесии, то бракованная монета — 5 коп. Если при втором взвешивании легче та же чашка, что и при первом взвешивании, то бракованная монета — 2 коп., в противном случае — 3 коп.
5. Замените в неравенствах
П > Р > О < Е < К < Т < И < Р > О > В > А > Н < И > Е буквы цифрами так, чтобы все неравенства стали верными (одинаковые буквы соответствуют одинаковым цифрам, разные — разным):
Ответ
Ответ. Н = 0, А = 1, В = 2, О = 3, Е = 4, К = 5, Т = 6, И = 7, Р = 8, П = 9.
Задачи четвёртого номера 1987 года
1. Замените на рисунке звёздочки цифрами так, чтобы равенство оказалось верным.
Ответ
Ответ. 292 · 211 = 61 612.
2. В 1987 году возраст старшего из двух братьев стал равен сумме цифр года рождения младшего, а возраст младшего — сумме цифр года рождения старшего брата. Сколько им лет, если один старше другого на 7 лет?
Ответ
Ответ. Старший брат родился в 1962 году, а младший — в 1969 году.
3. Однажды Петя попробовал подключить лампочку к двум батарейкам так, как показано на рисунке. Однако лампочка не загорелась, хотя от каждой из батареек она зажигалась. Почему?
Ответ
Ответ. Цепь на рисунке не замкнута, поэтому ток по ней не течёт.
4. Шофёр автобуса установил в одной кассе катушку билетов с номерами от 537 000 до 537 999, а в другой — с номерами от 462 000 до 462 999. В какой из катушек «счастливых» билетов больше (то есть таких, что сумма первых трёх цифр равна сумме следующих трёх цифр)?
Ответ
Указание
Решение
Ответ. Поровну.
Указание. Замените каждую цифру «счастливого» билета её дополнением до 9, то есть 0 на 9, 1 на 8 и так далее.
Решение. Если заменить каждую цифру «счастливого» билета её дополнением до 9, то есть 0 на 9, 1 на 8 и так далее, то полученный билет тоже будет «счастливым», причём если билет был из первой катушки, то полученный билет будет из второй катушки, и наоборот. Следовательно, в катушках одно и то же количество «счастливых» билетов.
5. Отрезок, соединяющий середины двух противоположных сторон выпуклого четырёхугольника, делит его на два четырёхугольника равной площади. Докажите, что эти стороны параллельны.
Указание
Решение
Указание. Соедините одну из середин сторон с вершинами противоположной стороны отрезками:
Решение. Соединим одну из середин сторон с вершинами противоположной стороны отрезками:
Площади синего и красного треугольников равны, поэтому равны и площади жёлтых треугольников. Следовательно, их высоты, опущенные на нижние стороны, равны, а это значит, что верхняя сторона четырёхугольника параллельна нижней.
Задачи пятого номера 1987 года
1. Сумма длин каких изображённых на рисунке полуокружностей больше: верхних или нижних?
Ответ
Решение
Ответ. Суммы длин равны.
Решение. Эти суммы длин равны произведению числа π/2 на длину отрезка.
2. Почему растения не рекомендуют поливать днём, особенно в солнечную погоду?
Ответ
Ответ. Капли воды, преломляя свет как линзы, концентрируют его в отдельных точках, что может привести к ожогам растения.
3. Совершите путешествие из пункта П в пункт Е рисунка. Для этого замените буквы цифрами так, чтобы все равенства стали верными (одинаковые буквы заменяют одинаковые цифры, разные — разные). Счастливого пути!
Ответ
Ответ. ПУ ТЕШ ЕСТ ВИЕ = 62 314 153 871.
4. Из шести косточек домино выложен прямоугольник так, что ему соответствует пример на сложение. Сложите из шести косточек домино (может быть, других) аналогичный прямоугольник так, чтобы сумма (то есть число в нижней строчке) была наименьшей.
Ответ
Ответ. Наименьшая сумма равна 102. Она достигается в следующих трёх расположениях:
5. В детском кафе стоят одинаковые круглые и одинаковые квадратные столы, на которых лежат одинаковые круглые и одинаковые квадратные салфетки. Круглый стол можно покрыть четырьмя квадратными салфетками, а квадратный — четырьмя круглыми салфетками. Докажите, что диаметр круглой салфетки не меньше половины диагонали квадратного стола, а сторона квадратной салфетки не меньше радиуса круглого стола.
Указание
Решение
Указание. В случае квадратного стола и круглых салфеток рассмотрите пять точек: четыре угла и центр.
Если квадратные салфетки покрывают круглый стол, то хотя бы одна из них покрывает не меньше четверти этой окружности.
Решение. В случае квадратного стола и круглых салфеток отметим на столе пять точек: четыре угла и центр. Так как салфеток четыре, хотя бы одна салфетка покрывает сразу две из этих точек. Из расстояний между этими точками
наименьшее — между центром и одним из углов.
Это — половина диагонали квадрата, поэтому диаметр круглой салфетки
не меньше этого расстояния.
Если квадратные салфетки покрывают круглый стол, то они покрывают и его край — окружность. Среди салфеток найдётся такая, которая покрывает не меньше четверти этой окружности.
Рассмотрите на этой дуге две точки, отстоящие друг от друга ровно на четверть окружности. Расстояние между ними не больше диагонали квадратной салфетки.
Задачи шестого номера 1987 года
1. Замените на рисунке буквы цифрами так, чтобы получились верные равенства. Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
Ответ
Ответ. 2 · 1 = 8 – 6 = 2 : 1 = 8 : 4 = 3 – 1.
2. Говорят, что Тортила отдала Буратино золотой ключик не так просто, как рассказал А.Н. Толстой, а вынесла три коробочки: красную, синюю и зелёную. На красной коробочке было написано «Здесь лежит золотой ключик», на синей — «Зелёная коробочка пуста», а на зелёной — «Здесь сидит гадюка». Тортила прочла надписи и сказала: «Действительно, в одной коробочке лежит золотой ключик, в другой — гадюка, а третья пуста, но все надписи неверны». Где же лежит золотой ключик?
Указание
Решение
Указание. В зелёной коробочке.
Решение. Вследствие ложности надписи на синей коробочке, зелёная коробочка непуста. Поскольку ложна надпись на зелёной коробочке, в ней нет гадюки. Значит, именно в зелёной коробочке лежит золотой ключик.
3. У Коли, Вити и Юры было 12, 14 и 22 ореха. Когда Коля отдал Вите столько орехов, сколько было у Вити, затем Витя отдал Юре столько орехов, сколько было у Юры, а Юра отдал Коле столько орехов, сколько оставалось у Коли, у всех ребят орехов оказалось поровну. Сколько орехов было у каждого?
Ответ
Ответ. У Коли 22 ореха, у Вити 14, у Юры — 12 орехов.
4. Лихие капитаны парусников, перевозивших хлопок из Австралии в Англию, не стремились полностью загружать свои корабли, хотя были заинтересованы в перевозке большего количества хлопка. Почему?
Ответ
Ответ. Хлопок впитывает влагу, поэтому при транспортировке по морю вес хлопка увеличивается. Капитаны загружали хлопок с учётом будущего увеличения его веса.
5. Выпуклый четырёхугольник разрезали по двум средним линиям (отрезкам, соединяющим середины противоположных сторон). Докажите, что из полученных четырёх частей можно сложить параллелограмм.
Указание
Ответ
Указание. Сумма величин углов четырёхугольника равна 360°.
Ответ. 
Задачи седьмого номера 1987 года
1. Дядя Алёша вдвое старше меня, а цифры числа, выражающего мой возраст, равны сумме и разности цифр его возраста. Сколько мне лет?
Ответ
Ответ. Дяде Алёше 34 года, а мне 17 лет.
2. Двери в салоне электрички движутся на роликах по направляющим, расположенным не горизонтально, а наклонно. Почему?
Указание
Ответ
Указание. Чаще всего во время движения электрички двери в салоне закрыты.
Ответ. Открытые кем-либо двери сами закрываются, скатываясь по направляющим под действием силы тяжести.
3. Во время новогоднего карнавала Антон забежал в свой класс и увидел оставшийся на доске пример на возведение числа в пятую степень. Он стёр три цифры у результата и получил: **198*7. (Звёздочки стоят на местах стёртых цифр.) Какое число возвели в пятую степень?
Ответ
Указание
Решение
Ответ. 17.
Указание. Пятая степень любого числа оканчивается той же цифрой, что и само число.
Решение. Пятая степень числа 10 слишком мала, а пятая степень числа 30 равна 24 300 000 и слишком велика. Поскольку пятая степень любого числа оканчивается той же цифрой, что и само число, под подозрением два числа: 17 и 27. Число 275 = 14 348 907 восьмизначное, а 175 = 1 419 857; следовательно, ответ — число 17.
4. Зашнуровать спортивные туфли так, как изображено на рисунке, можно многими способами за счёт различий в шнуровке изнутри. Сколько же таких способов?
Ответ
Решение
Ответ. 384.
Решение. Начнём шнуровать с правой верхней дырочки. Можно пропустить шнурок в любую из дырочек, кроме второй верхней дырочки, то есть 8 способами. Следующим шагом продеваем шнурок в дырочку напротив — снова выбор, теперь уже из 6 возможностей, потом, после ещё двух пропусканий шнурка, останется 4 возможности, потом 2, наконец, единственным способом пропускаем шнурок в левую верхнюю дырочку. Всего 8 · 6 · 4 · 2 = 384 способа.
5. Однажды на лестнице я нашёл странную тетрадь. В ней было написано сто следующих утверждений:
«В этой тетради ровно одно неверное утверждение.»;
«В этой тетради ровно два неверных утверждения.»;
. . . . . . . . . . . .
«В этой тетради ровно сто неверных утверждений.».
Какое же из этих утверждений верное?
Ответ
Решение
Ответ. 99-е.
Решение. Сначала убедимся, что написано не более одного верного утверждения: если бы их было больше, то любые два из них противоречили бы друг другу и, следовательно, не могли бы быть одновременно верными. Все утверждения не могут быть неверными, так как в таком случае последнее утверждение было бы верным, что противоречит предположению. Итак, верно лишь одно утверждение, а именно 99-е, которое утверждает, что неверно 99 утверждений, а верно одно — оно само.
Задачи восьмого номера 1987 года
1. Пусть a и b — две разные цифры, цифра a не равна нулю. Докажите, что равенство
а) (10a + b) (100a + 10a + a) = (100a + 10b + a) (10a + a) не выполнено ни при каких a и b;
б) (10a + b) (100a + 10a + a) = (100a + 10b + a) (10a + a) + 1 выполнено лишь для одной пары цифр a и b;
в) (10a + b) (1000a + 100a + 10a + a) = (1000a + 100b + 10a + b) (10a + a)
выполнено всегда.
Решение
Решение. а) Правая часть делится на 11, а левая — нет.
б) Левая часть делится на a, а правая — лишь при a = 1; значит, a = 1; из уравнения
111(10 + b) = 11(101 + 10b) + 1
находим b = 2.
в) Левая и правая части равны произведению чисел 10a + b, 11a и 101.
2. Разложите все 28 косточек домино в четыре кучки так, чтобы суммы очков в кучках были четырьмя последовательными простыми числами.
Указание I
Указание II
Указание I. Найдите сумму всех очков.
Указание II. Сумма всех очков равна
6(0+1+2+3+4+5+6) = 168,
а 37 + 41 + 43 + 47 = 168.
3. Решите числовой ребус
СЛОВ,О + СЛОВ,О = ПЕСНЯ.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
Ответ
Ответ. 9453,5 + 9453,5 = 18 907.
4. Стрелку компаса укрепили на плоской пробке и опустили пробку в воду. Как будет вести себя пробка?
Ответ
Ответ. Магнитное поле Земли оказывает ориентирующее действие на стрелку компаса. Если бы жёстко скреплённую с пробкой стрелку поставили не на воду, а на шероховатую твёрдую поверхность, то сила трения покоя не дала бы пробке развернуться так, чтобы стрелка указывала на север. В воде же сила трения покоя отсутствует; поэтому под действием магнитного поля Земли опущенная на воду пробка с закреплённой на ней стрелкой компаса начнёт совершать колебания около направления на север. В конце концов из-за сопротивления воды эти колебания затухнут, и стрелка будет указывать на север.
5. Подставьте вместо многоточий на рисунке цифры или числа так, чтобы предложение оказалось верным.
Ответ
Ответ. Здесь присутствуют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, причём
0 — 2 раза,
1 — 2 раза,
2 — 8 раз,
3 — 4 раза,
4 — 3 раза,
5 — 2 раза,
6 — 2 раза,
7 — 2 раза,
8 — 3 раза,
9 — 2 раза.
Задачи девятого номера 1987 года
1. Решите арифметический ребус
РАЙОН + РАЙОН = ГОРОД.
Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
Ответ
Ответ. 45 203 + 45 203 = 90 406.
2. Как-то раз я уронил термометр, которым обычно измеряю температуру фотореактивов. Термометр не разбился, но столбик спирта «разорвался». Как починить термометр?
Ответ
Ответ. Достаточно поместить термометр в хороший морозильник. Спирт сократится и весь втянется в колбочку. После нагревания новый столбик спирта будет уже без разрывов.
3. Коля купил в буфете 3 пакетика ирисок. Витя — 2 пакетика. Когда пришёл в буфет Алёша, ирисок уже не было. Друзья разделили купленные ириски поровну. Выяснилось, что Алёша должен друзьям 25 копеек. Сколько стоил пакетик ирисок и сколько Алёша должен Коле, а сколько — Вите?
Ответ
Решение
Ответ. Пакетик ирисок стоит 15 копеек, Алёша должен Коле 20 копеек, а Вите — 5 копеек.
Решение. Поскольку доля Алёши составляет 25 копеек, таковы же доли Коли и Вити. Значит, все 5 пакетиков ирисок стоят 75 копеек, а один пакетик — 15 копеек. Коля заплатил 45 копеек, поэтому он должен получить 45 – 25 = 20 копеек, а Витя — остальные 30 – 25 = 5 копеек.
4. Городские часы отбивают каждый час положенное число раз. Кроме того, они бьют один раз в половину каждого часа. Анатолий Павлович любит читать книгу, сидя в скверике около курантов. Однажды за время, пока он читал, часы принимались бить пять раз, а всего он насчитал 11 ударов. С последним ударом часов Анатолий Павлович встал и пошёл домой. В какое это было время?
Ответ
Решение
Ответ. В 4 часа дня.
Решение. Поскольку часы принимались бить пять раз, то получасовых ударов было 2 или 3. Если их было 3, то на два соседних часа приходится 8 ударов; в одном случае чётное число ударов, а в другом нечётное, то есть в сумме 8 ударов быть не может. Если было 2 получасовых удара, то оставшиеся 9 ударов однозначно представимы в виде суммы трёх последовательных чисел: 2 + 3 + 4. Анатолий Павлович ушёл в 4 часа дня.
5. Может ли какая-нибудь степень двойки содержать в своей записи поровну нулей, единиц, двоек, ..., девяток?
Ответ
Указание
Решение
Ответ. Не может.
Указание. Рассмотрите сумму цифр.
Решение. Сумма 0 + 1 + 2 + ... + 9 = 45 делится на 9. Если бы степень двойки имела поровну нулей, единиц и так далее, то сумма цифр делилась бы на 9; следовательно, и само число должно делиться на 9, а оно делится только на степени числа 2.
Задачи десятого номера 1987 года
1. Нетрудно доказать, что сумма величин углов правильной пятиконечной звезды равна 180°. Докажите, что такова же сумма углов произвольной пятиконечной звезды.
Указание I
Указание II
Указание III
Указание IV
I способ
II способ
III способ
IV способ
Указание I. Рассмотрите треугольник
CPQ и примените теорему о внешнем угле треугольника к некоторым двум треугольникам для сведения задачи о подсчёте суммы величин углов звезды к задаче о подсчёте суммы величин углов треугольника.
Указание II. Соедините две соседние вершины звезды, например
A и
E, и сведите дело к подсчёту суммы величин углов треугольника
ACE.
Указание III. Рассмотрите сумму величин внешних углов закрашенного пятиугольника.
Указание IV. Рассмотрите окружность, внутри которой лежит пятиугольная звезда, продолжите стороны звезды до пересечений с окружностью и примените теорему об угле между хордами.
I способ. В силу теоремы о внешнем угле треугольника
APD, сумма величин углов
A и
D пятиугольной звезды равна величине угла
CPQ; аналогично, в силу теоремы о внешнем угле треугольника
BQE, сумма величин углов
B и
E пятиугольной звезды равна величине угла
CQP. Следовательно, сумма величин углов пятиугольной звезды равна сумме величин углов треугольника
CPQ.
II способ. Соединим две соседние вершины звезды, например
A и
E.
Так как у треугольников AME и BMD углы при вершине M конгруэнтны, сумма величин углов при вершинах B и D треугольника BMD равна сумме величин углов при вершинах A и E треугольника AME; но тогда сумма величин углов при вершинах звезды равна сумме величин углов треугольника ACE, то есть 180°.
III способ. Сумма величин углов закрашенного пятиугольника равна
3 · 180° = 540°.
Поэтому сумма величин внешних углов равна 5 · 180° – 540° = 360°, тоудвоенная сумма величин внешних углов равна 2 · 360° = 720°, а искомая сумма величин углов пятиугольной звезды равна 5 · 180° – 720° = 180°.
IV способ. Рассмотрим окружность, внутри которой лежит пятиугольная звезда. Поскольку величина угла между хордами окружности равна полусумме величин соответствующих дуг, то сумма величин углов звезды равна половине от 360°,
то есть 180°.
2. Мне удалось, взяв по два раза цифры 1, 2, 3 и 4, написать восьмизначное число, у которого между единицами стоит одна цифра, между двойками — две, между тройками — три, а между четвёрками — четыре цифры. А вы так можете?
Ответ
Комментарий
Ответ. Например, 41312432.
Комментарий. Можно доказать, что таких чисел два: 41312432 и 23421314. Одно из них получается из другого чтением в обратном направлении.
3. Расставьте числа от 1 до 8 в кружках изображённой на рисунке фигуры так, чтобы числа в кружках, соединённых отрезками, отличались не меньше, чем на два.
Указание
Решение
Указание. Каждый из двух центральных кружочков соединён с шестью кружочками. Поэтому в центральных кружочках не могут быть никакие цифры, кроме 1 и 8.
Решение. Каждый из двух центральных кружочков соединён с шестью кружочками. Поэтому в центральных кружочках
не могут быть никакие цифры, кроме 1
и 8. После этого однозначно определяются положения чисел 2
и 7, затем — положение
числа 3 и остальных.
4. Мои настенные часы ведут себя очень странно. В первой половине каждого часа они спешат на две минуты, зато во второй его половине на две минуты отстают. В чём причина такого поведения часов?
Ответ
Ответ. Часы идут точно, но минутная стрелка плохо закреплена на своей оси: она может свободно отклоняться от правильного положения на 2 минуты в одну или другую сторону. Часы висят на стене и под действием силы тяжести стрелка располагается ниже своего нормального положения. В правой части циферблата это приводит к опережению на две минуты, а в левой — к отставанию. Нужно закрепить минутную стрелку.
5. Точка, взятая внутри равностороннего треугольника, соединена со всеми вершинами. Кроме того, из неё опущены перпендикуляры на все стороны треугольника. Докажите, что сумма площадей красных треугольников равна сумме площадей синих треугольников.
Указание
Решение
Указание. Проведите через данную точку прямые параллельно сторонам треугольника до пересечений со сторонами:
Решение. Проведём через данную точку прямые параллельно сторонам треугольника до пересечений со сторонами:
Возникают шесть пар конгруэнтных треугольников:
Задачи одиннадцатого номера 1987 года
1. После окончания шахматного турнира в один круг (каждый сыграл с каждым другим по одному разу) все пять его участников А, Б, В, Г, Д, перечисленные здесь в порядке занятых мест, обменялись впечатлениями.
— Не думал, что лишь я один не испытаю горечи поражения,— сказал Б.
— А вот мне единственному не удалось одержать ни одной победы,— заметил Д.
Попробуйте по этим данным восстановить турнирную таблицу: выясните о каждых двух игроках, как именно окончились их партия.
2. Почему в морозный день снег скрипит под ногами?
Ответ
Ответ. В морозный день кристаллы снега разрастаются. Они ломаются при наступании на снег, что и вызывает потрескивание.
3. Расшифруйте ребус
ДЕДКА + БАБКА + РЕПКА = СКАЗКА,
в котором одинаковым буквам соответствуют одинаковые цифры, разным — разные, и ДЕДКА > БАБКА > РЕПКА.
Ответ
Ответ. 94 950 + 80 850 + 74 350 = 250 150.
4. Из набора гирек с массами 1 г, 2 г, ..., 101 г потерялась гирька массой 19 г. Можно ли оставшиеся 100 гирек разложить на две кучки по 50 штук в каждой так, чтобы массы кучек были одинаковы?
Ответ
Решение
Ответ. Да, можно.
Решение. Рассмотрим 18 пар гирек, равноотстоящих от концов: 1 + 101, 2 + 100, 3 + 99, ..., 18 + 84. Остальные 64 гирьки тоже разобьём на 32 пары, соединяя их по тому же принципу равной суммы: 20 + 83, 21 + 82, 22 + 81, ..., 51 + 52. Взяв 9 пар гирек из первого набора и 16 пар из второго произвольным образом, мы получим требуемое разбиение.
5. В равнобедренном треугольнике отмечены середины боковых сторон и их проекции на основание. Через отмеченные точки проведены две прямые, как показано на рисунке. Докажите, что из полученных частей можно сложить ромб.
Указание
Указание. 
Задачи двенадцатого номера 1987 года
1. Про три простых числа известно, что одно из них равно разности кубов двух других. Какие это числа?
Ответ
Решение
Ответ. 19 = 33 – 23.
Решение. Пусть это числа
p,
q и
r, причём
p = q3 – r3. Тогда
p = (q – r)(q2 + qr + r2).
Чтобы число p было простым, необходимо равенство
q – r = 1,
а оно возможно для простых чисел q и r лишь в случае q = 3 и r = 2. Число 33 – 23 = 19 действительно простое.
2. В некоторых старинных часах, предназначенных для работы на открытом воздухе, маятник изготовляли в виде длинной трубки, заканчивающейся сосудом со ртутью. С какой целью это делали?
Ответ
Ответ. При повышении температуры длина маятника увеличивается; ртуть, увеличиваясь в объёме, поднимается вверх по трубке, что при подборе объёма ртути и диаметра трубки даёт возможность сохранить постоянным расстояние от точки подвеса маятника до его центра тяжести. Тем самым увеличивается точность хода часов.
3. Решите числовой ребус, изображённый на рисунке. Одинаковым буквам соответствуют одинаковые числа, разным — разные.
Ответ
Ответ. 331 868 : 163 = 2036.
4. На хуторе Семидворье семь домов. Любопытно, что какие бы три дома мы ни выбрали, расстояние хотя бы между некоторыми двумя из трёх выбранных равно 100 метрам. Придумайте, как могут располагаться дома!
5. Тартарен, путешествуя по Африке, однажды остановился на ночлег на берегу небольшого озера с чистейшей водой (на дне били ключи). Однако утром к озеру подошло стадо слонов. Тартарен насчитал 183 головы. На следующее утро они ушли, оставив вместо озера грязную лужу. Через несколько лет Тартарен вновь попал на это место. Озеро вновь было полно воды, но утром опять появились слоны. На этот раз в стаде было 37 слонов, и воды им хватило на 5 дней. Покидая берега выпитого до дна озера, Тартарен задумался: за сколько дней опустошил бы озеро один слон?
