Комплексные числа

Рассмотрим плоскость с заданной на ней декартовой системой координат. Ось абсцисс назовём вещественной осью, ось ординат — мнимой осью.

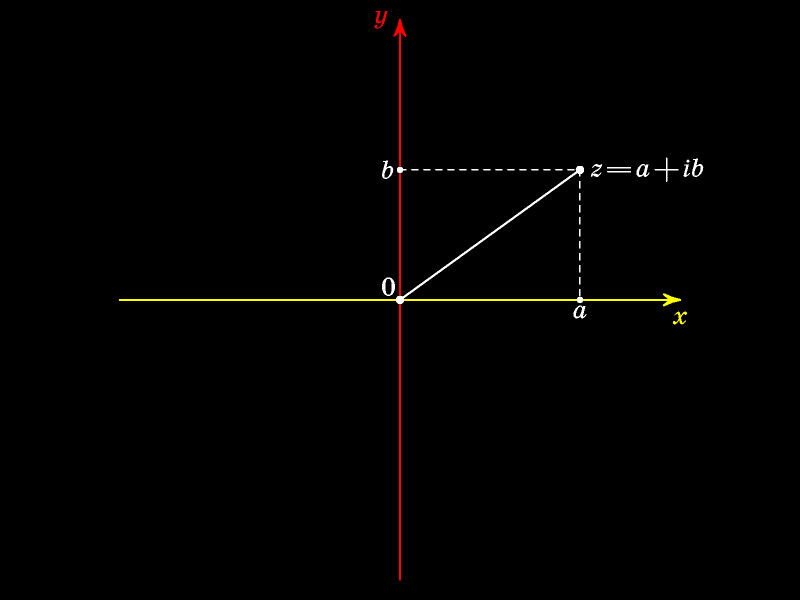
Точку (a; b) называют комплексным числом z = a + bi. Число a — вещественная часть, а число b — мнимая часть комплексного числа z. Запись a + bi называют алгебраической формой комплексного числа z.

Число -z симметрично числу z относительно начала координат.

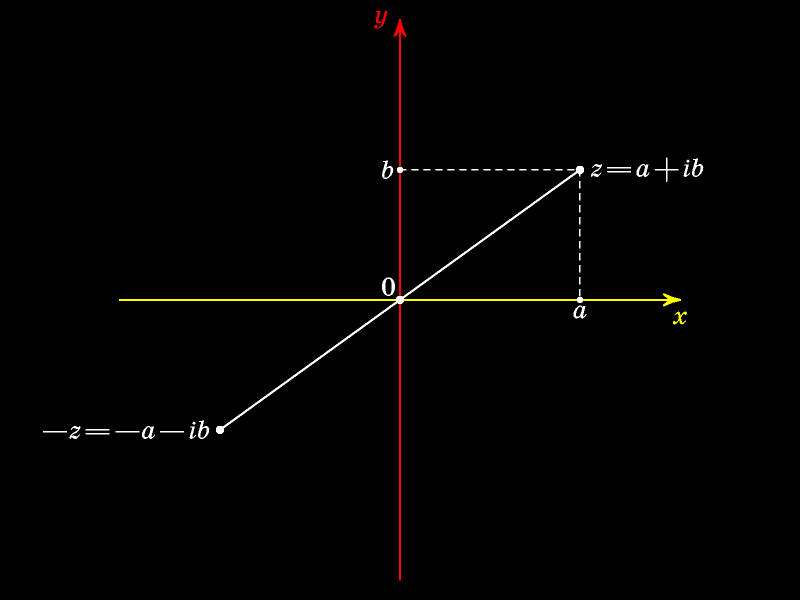
Число, симметричное числу z относительно оси абсцисс, называют сопряжённым к числу z.

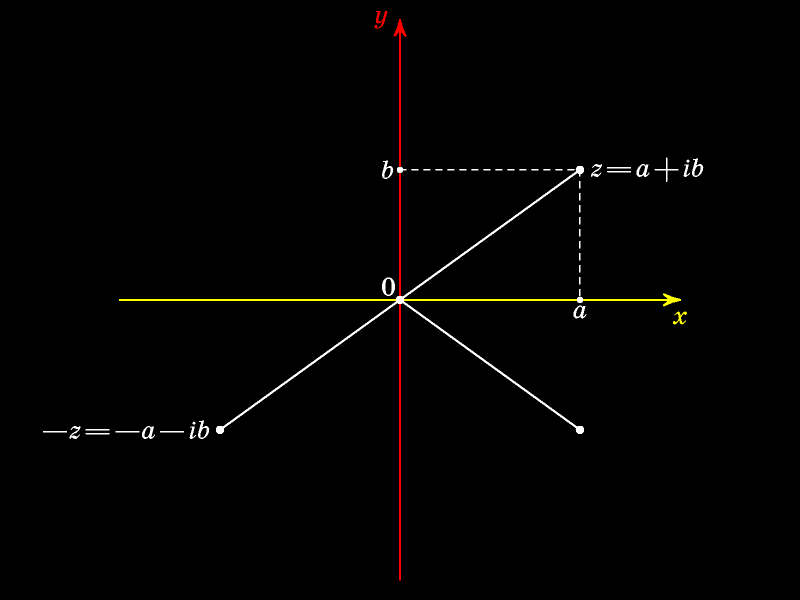
Это число a - bi обозначают так: z.

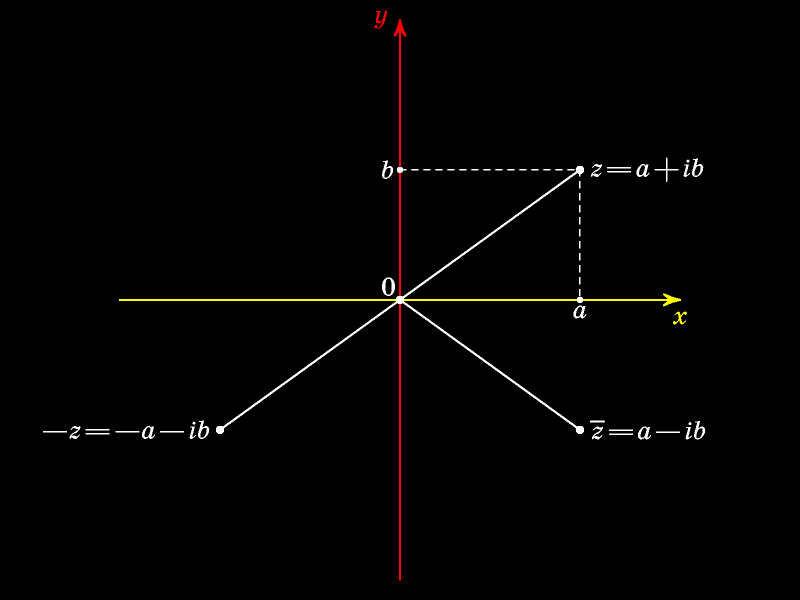
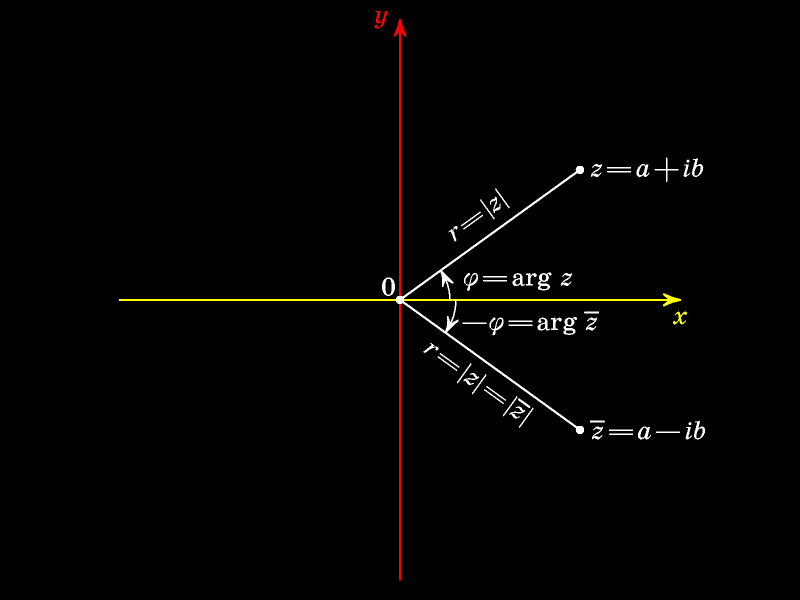
Модулем (абсолютной величиной) комплексного числа z называют расстояние от начала координат до точки (a; b).

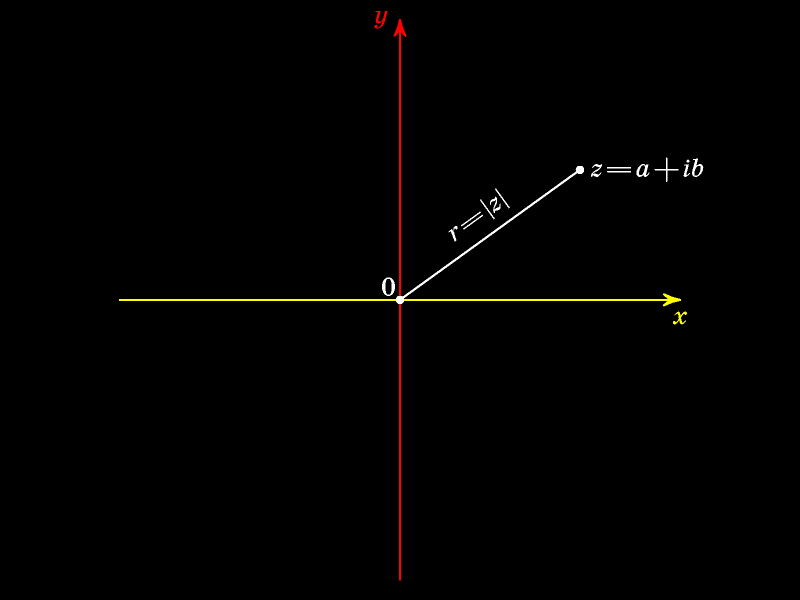
Аргумент числа — величина угла (отсчитываемого против часовой стрелки) между положительным направлением оси абсцисс и лучём, выходящим из начала координат и проходящим через точку (a; b). Аргумент определён с точностью до 360 градусов. Аргумент нуля (начала координат) не существует.

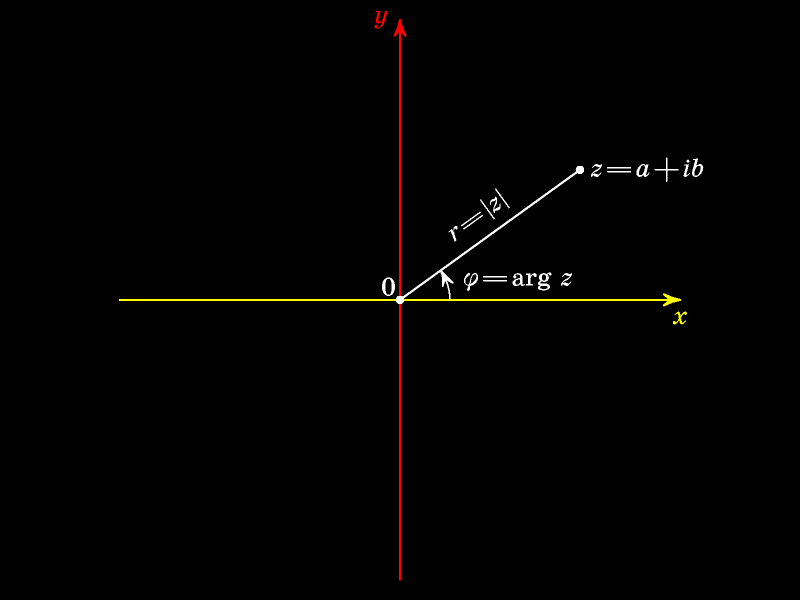
Модули сопряжённых чисел равны, а аргументы противоположны.

Как складывать и умножать комплексные числа z = a + bi и w = c + di?

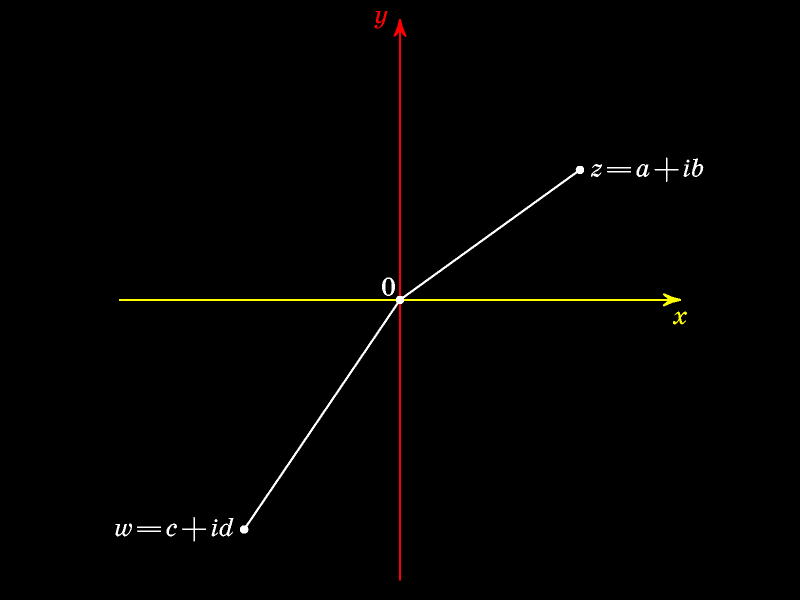
Сумма комплексных чисел — это сумма векторов.

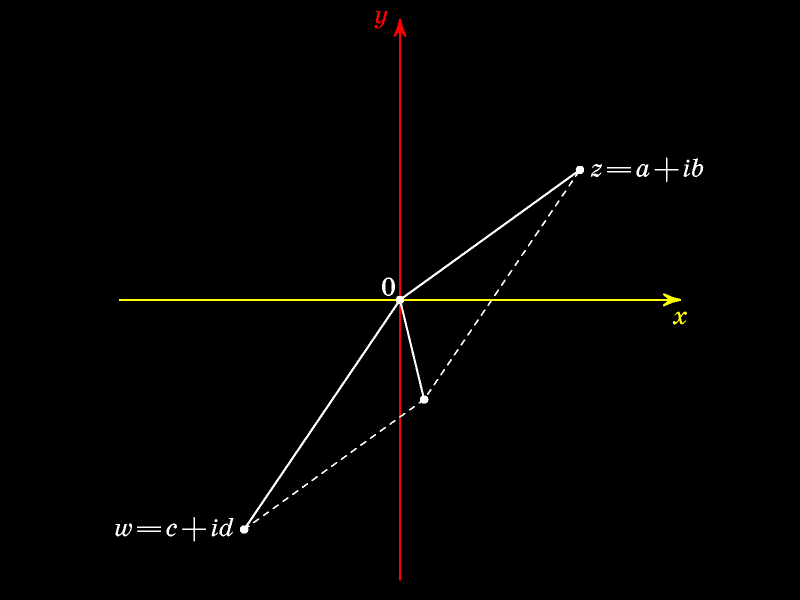
В алгебраической форме: z + w = (a + c) + (b + d)i.

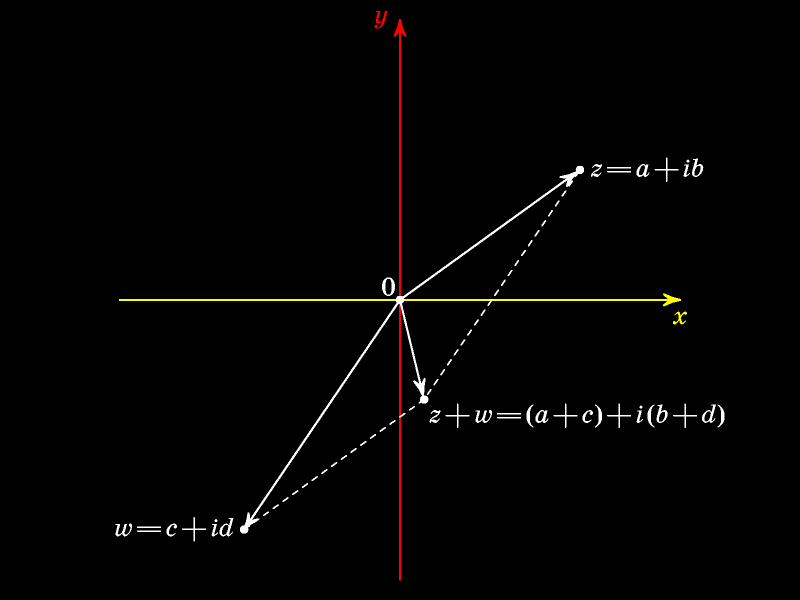
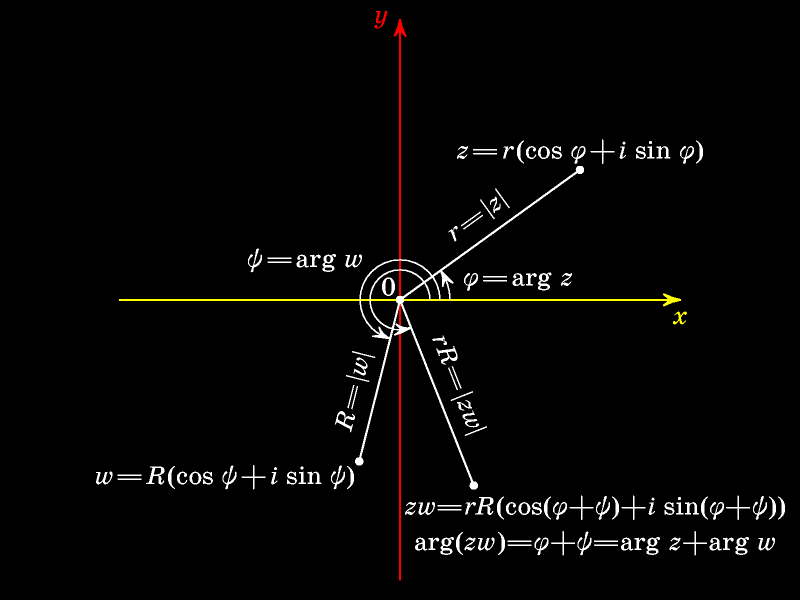
Тригонометрическая форма комплексного числа — это его выражение z = r(cos φ + i sin φ) через абсолютную величину r и аргумент φ комплексного числа z.

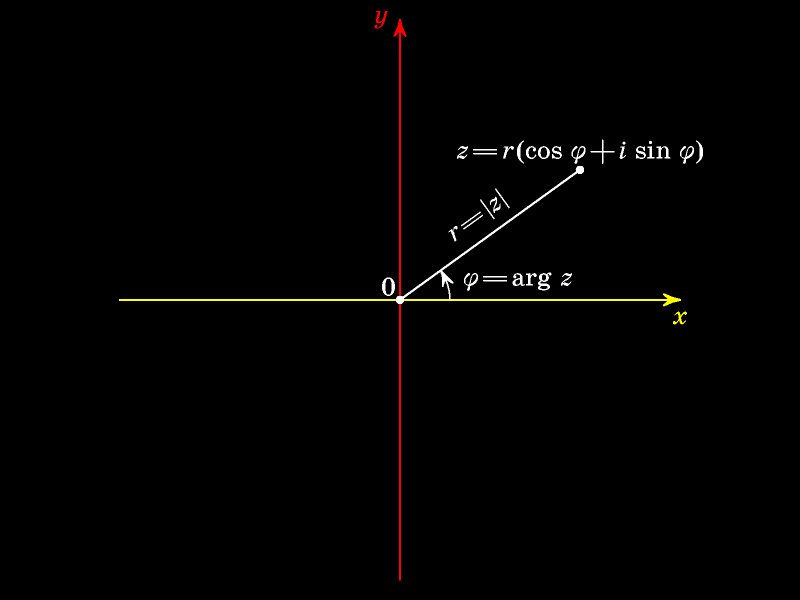
Научимся умножать комплексные числа, заданные в тригонометрической форме.

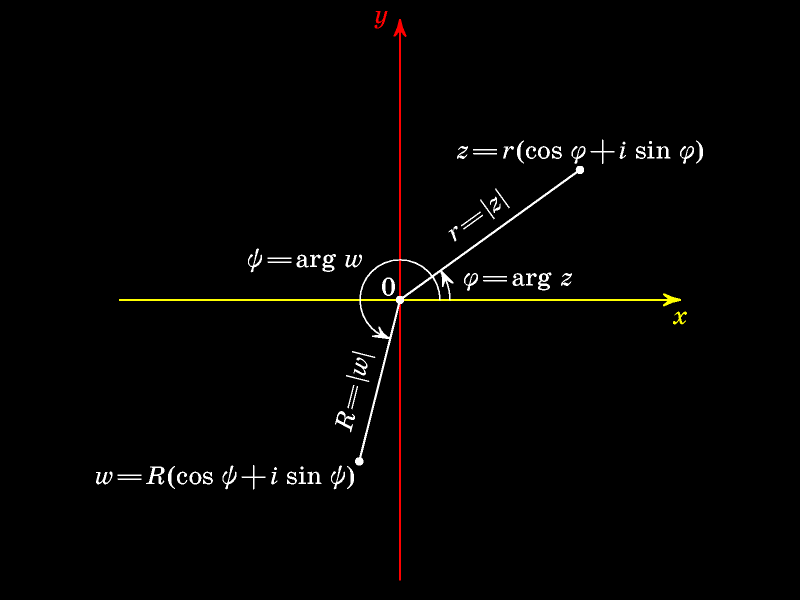
Для этого проведём луч из начала координат и через точку z.

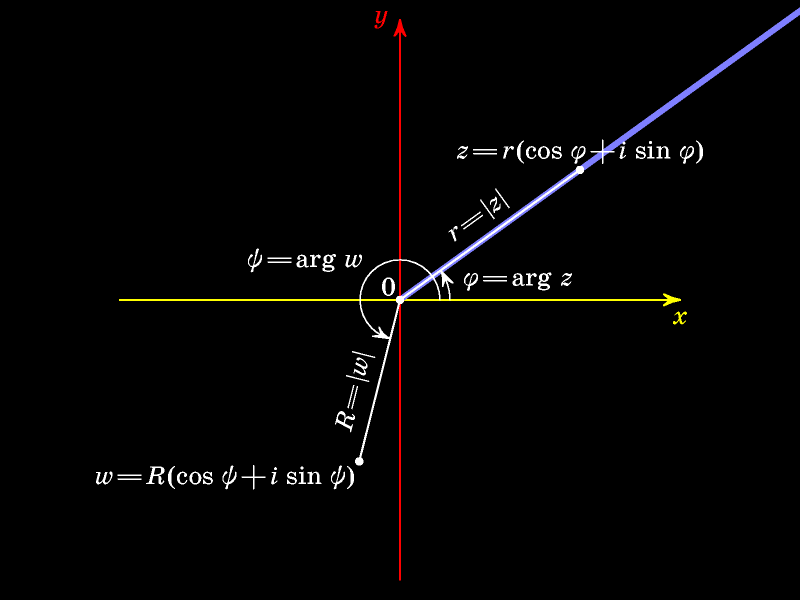
Отметим угол между положительным направлением оси абсцисс и проведённым лучом.

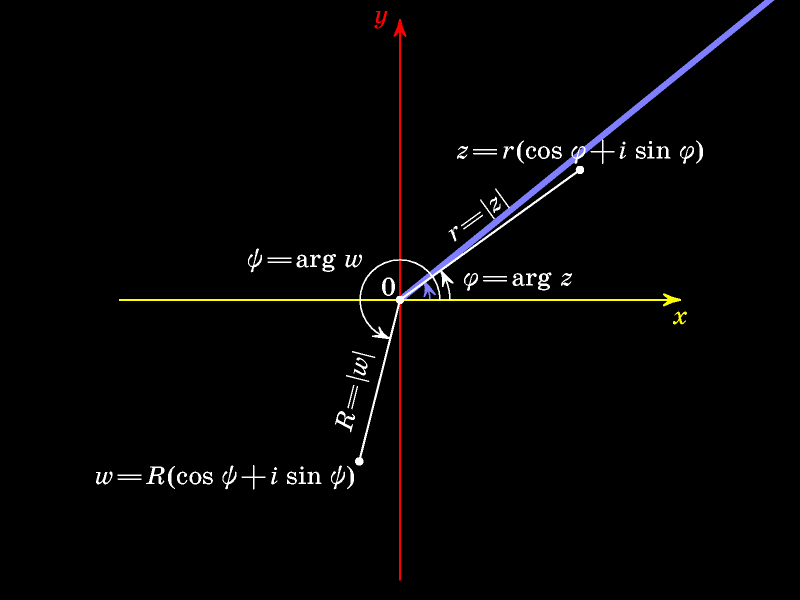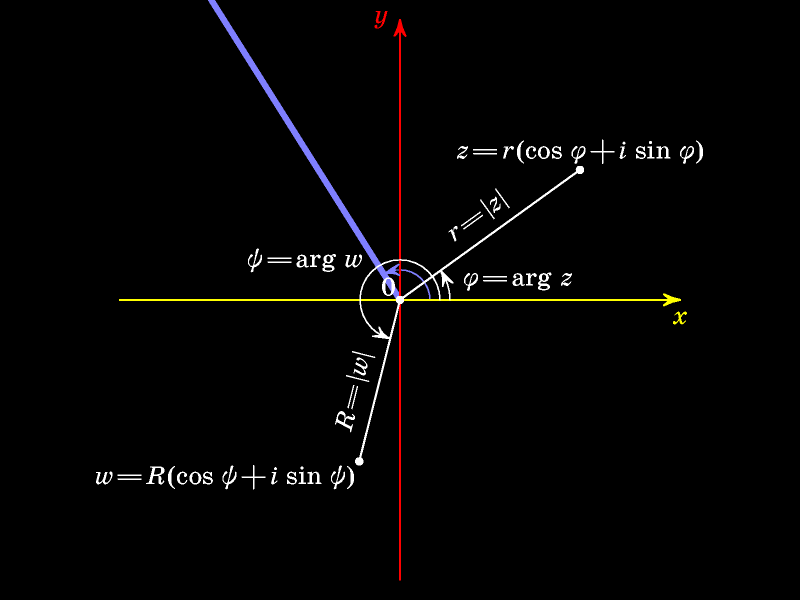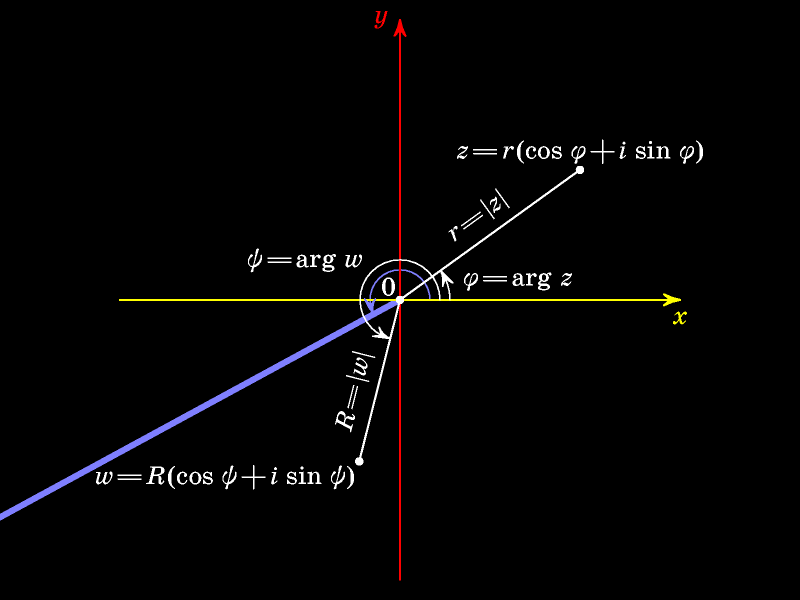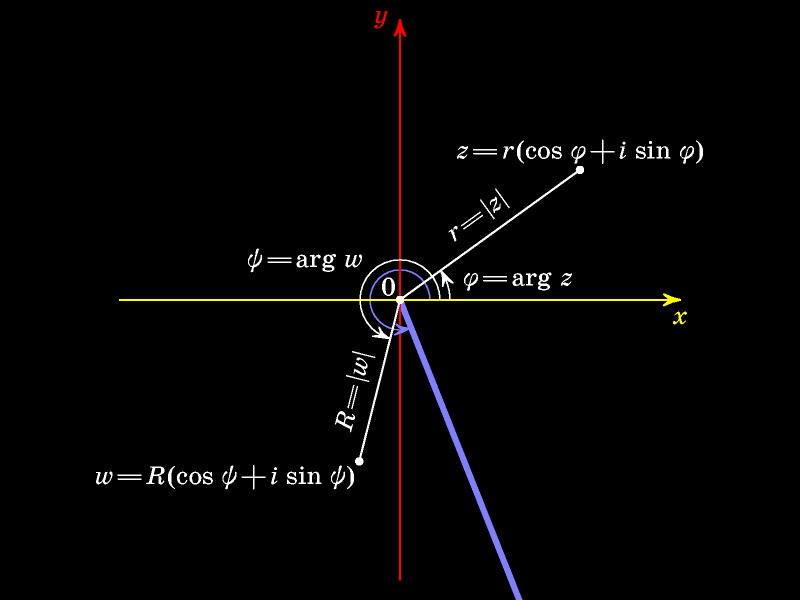
Увеличим этот угол на угол arg w.

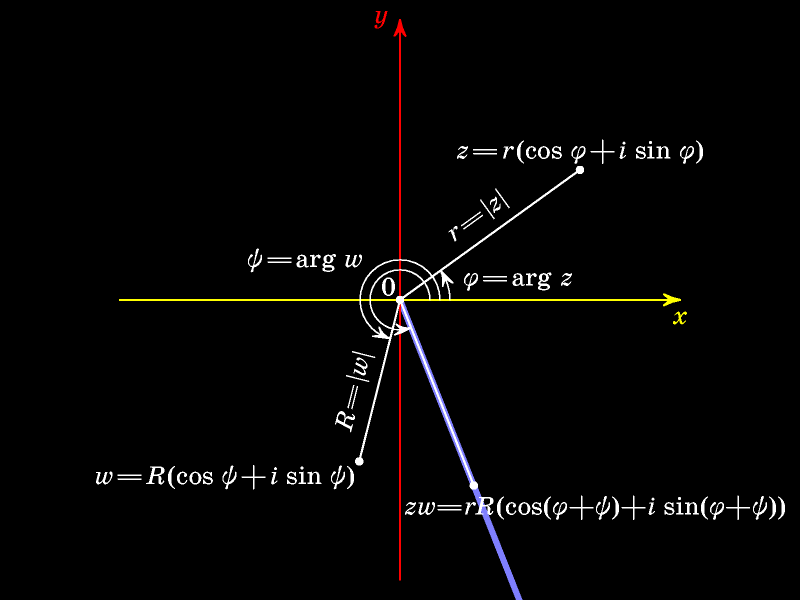
Модуль произведения равен произведению модулей сомножителей, а аргумент — сумме аргументов.

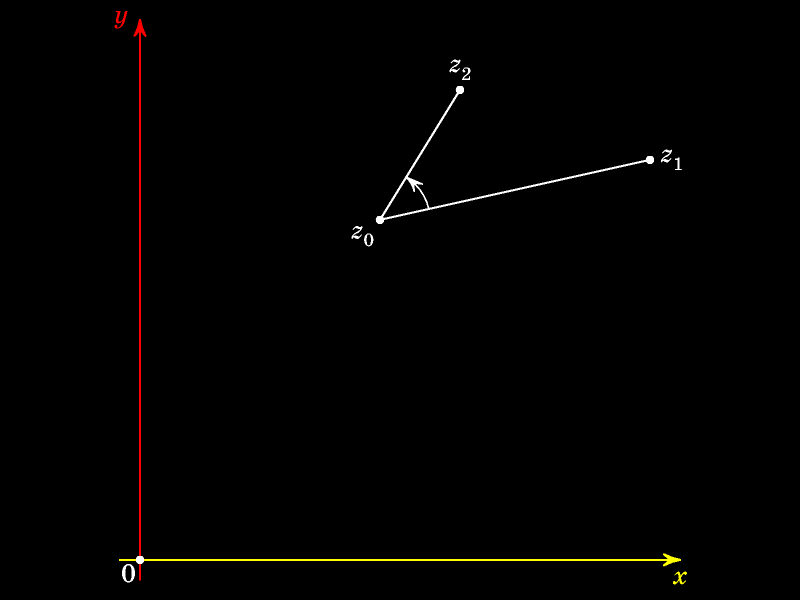
Рассмотрим три комплексных числа.

Построим угол z₁z₀z₂.

Выполним параллельный перенос на вектор -z₀, переводящий вершину угла в начало координат.

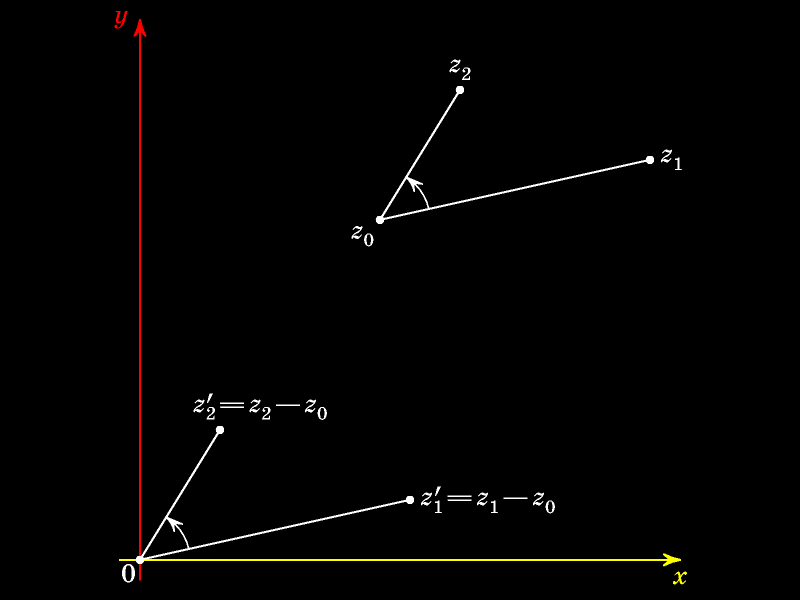
Величина угла равна разности аргументов чисел z₂ – z₀ и z₁ – z₀. Поэтому она равна аргументу частного (z₂ – z₀)/(z₁ – z₀).

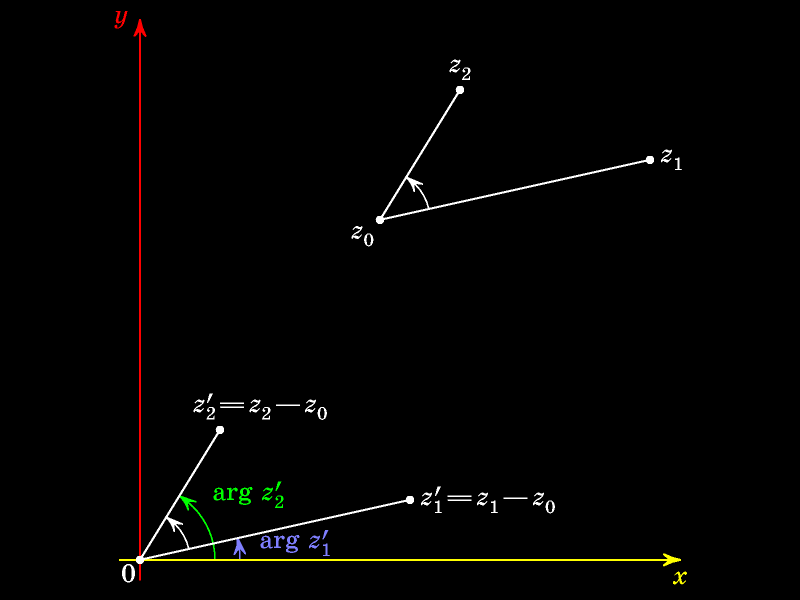
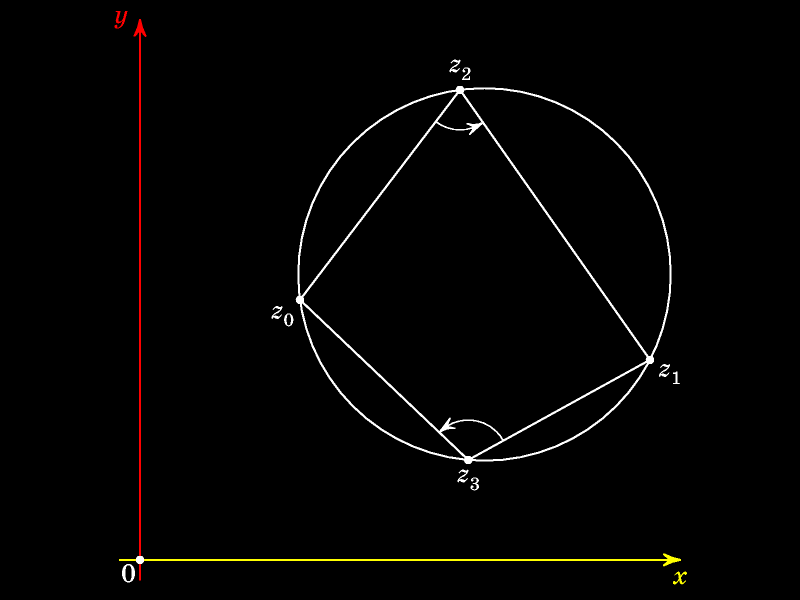
Построим описанную окружность треугольника с вершинами z₀, z₁ и z₂.

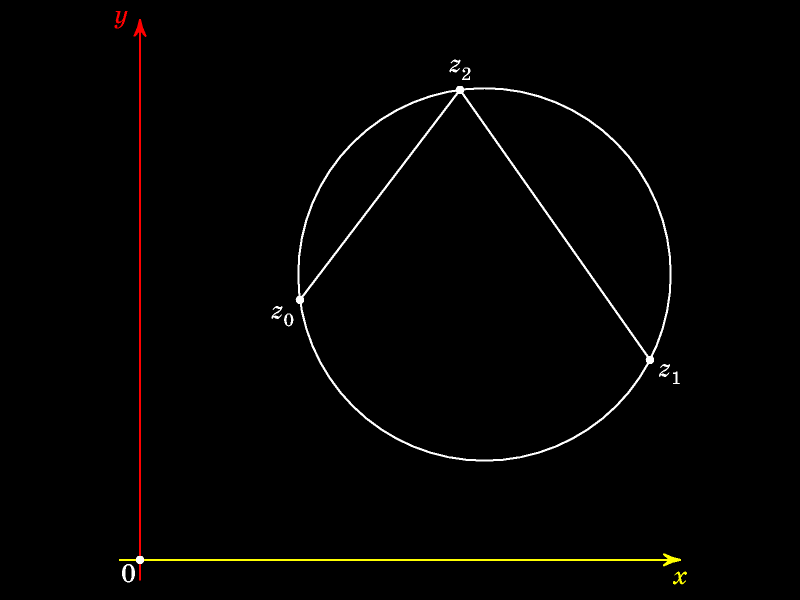
На этой окружности отметим произвольную точку z₃.

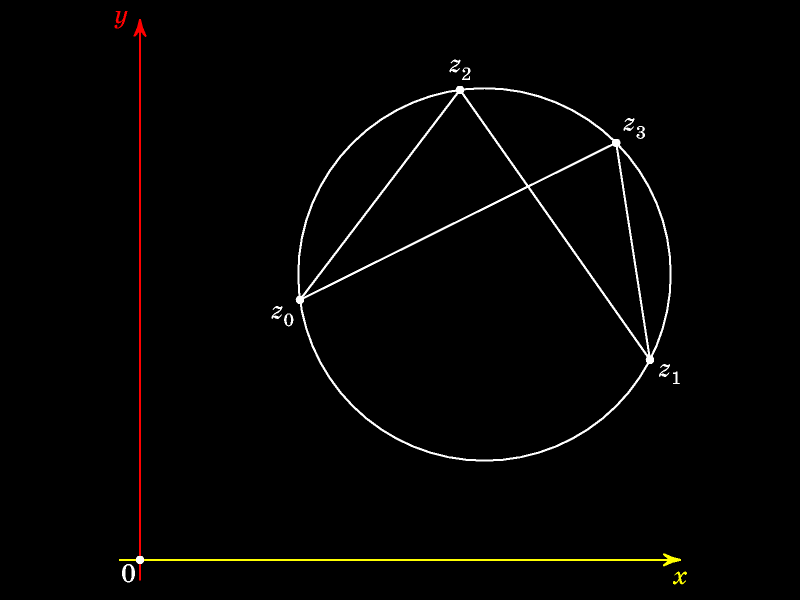
В силу теоремы о вписанном угле величины углов, опирающихся на одну и ту же дугу окружности, равны: arg ((z₁ – z₂)/(z₀ – z₂)) = arg ((z₁ – z₃)/(z₀ – z₃)). Это равенство выполнено тогда и только тогда, когда четыре точки лежат на одной окружности, причём z₂ и z₃ лежат по одну сторону от прямой, проходящей через точки z₀ и z₁.

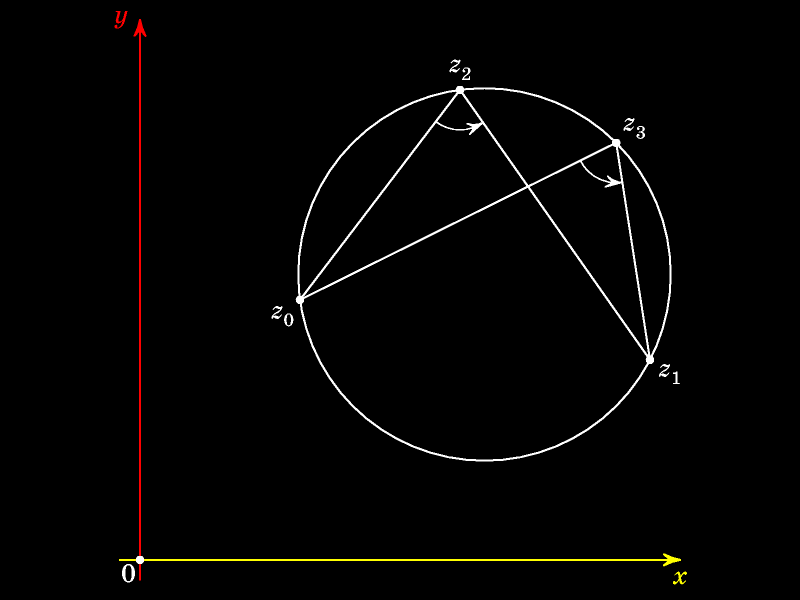
В ситуации, когда точки z₂ и z₃ лежат на разных дугах, на которые окружность разделена точками z₀ и z₁, равенство arg ((z₁ – z₂)/(z₀ – z₂)) = arg ((z₁ – z₃)/(z₀ – z₃)) не выполнено: аргументы чисел (z₁ – z₂)/(z₀ – z₂) и (z₁ – z₃)/(z₀ – z₃) не равны, а отличаются на 180 градусов. Таким образом, четыре разных комплексных числа лежат на одной окружности тогда и только тогда, когда двойное отношение — частное от деления числа (z₁ – z₂)/(z₀ – z₂) на число (z₁ – z₃)/(z₀ – z₃) — является вещественным числом.