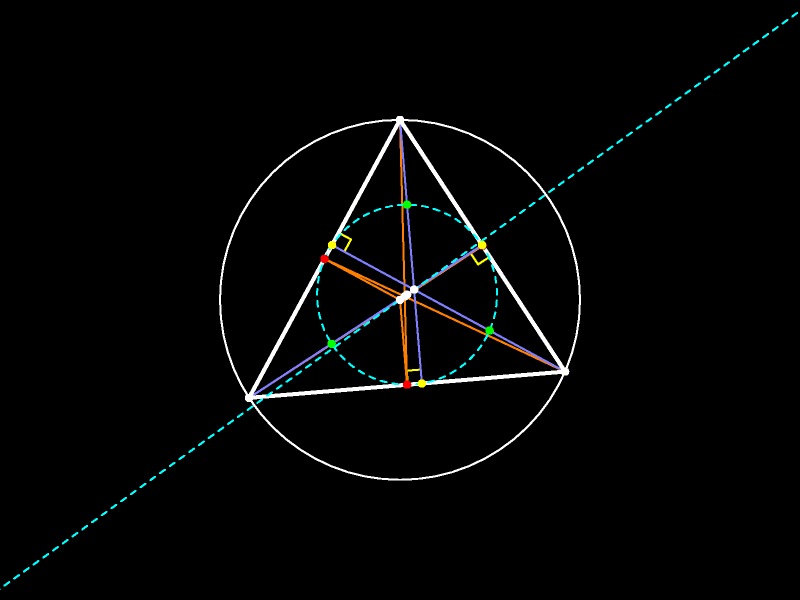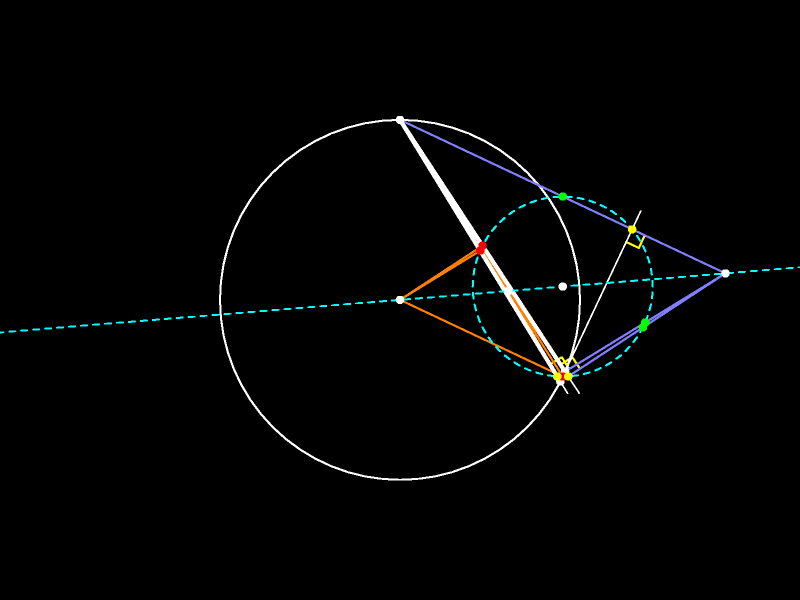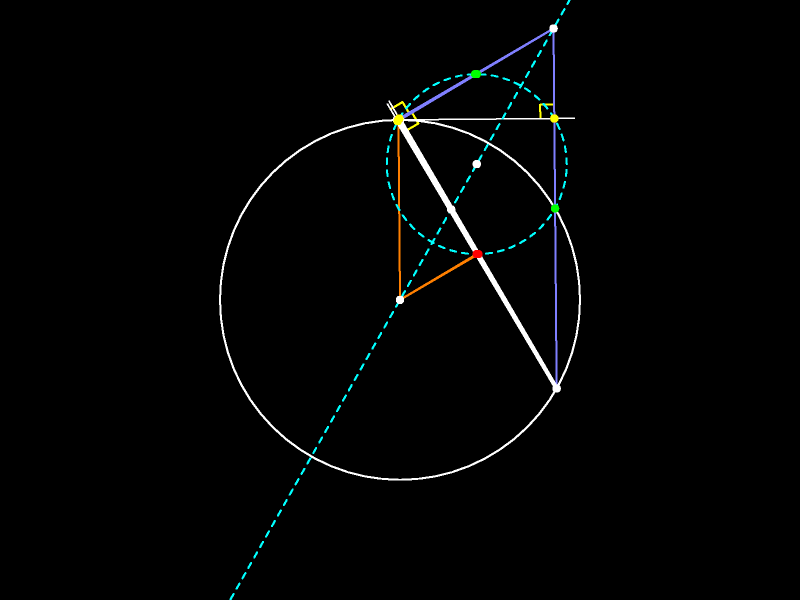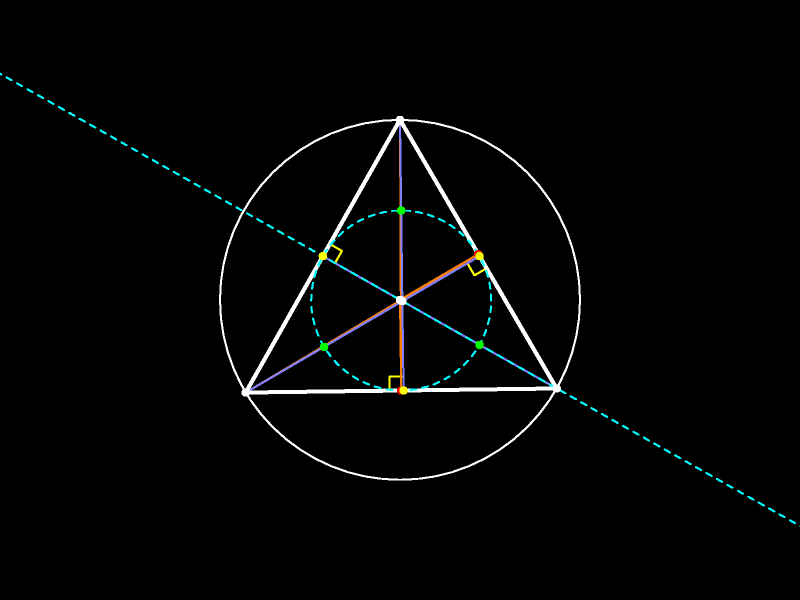
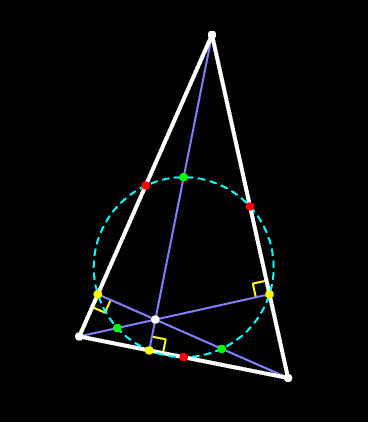
 Рассмотрим произвольный треугольник. Теорема Эйлера об окружности девяти точек гласит: основания высот, середины сторон и середины отрезков, соединяющих
Рассмотрим произвольный треугольник. Теорема Эйлера об окружности девяти точек гласит: основания высот, середины сторон и середины отрезков, соединяющих  Рассмотрим произвольный треугольник. Теорема Эйлера об окружности девяти точек гласит: основания высот, середины сторон и середины отрезков, соединяющих
Рассмотрим произвольный треугольник. Теорема Эйлера об окружности девяти точек гласит: основания высот, середины сторон и середины отрезков, соединяющих
Непрерывно изменяя исходный треугольник, получаем мультфильм.
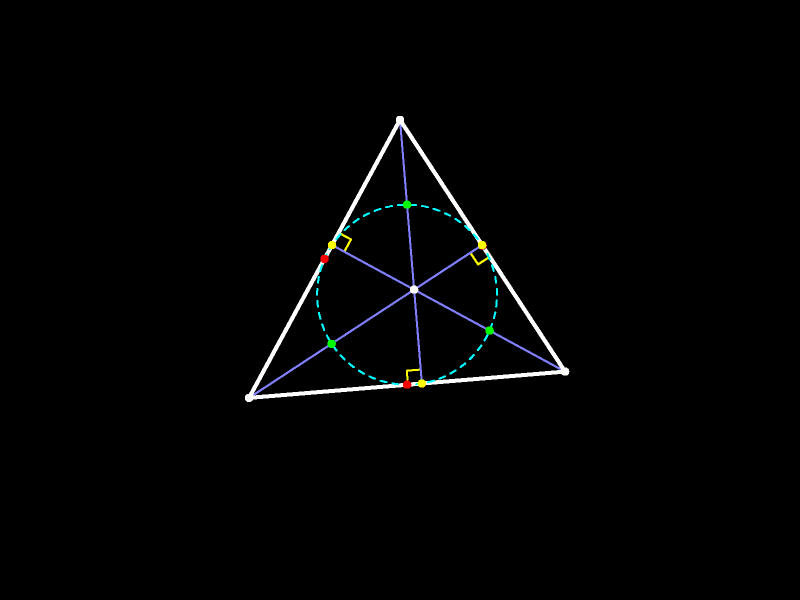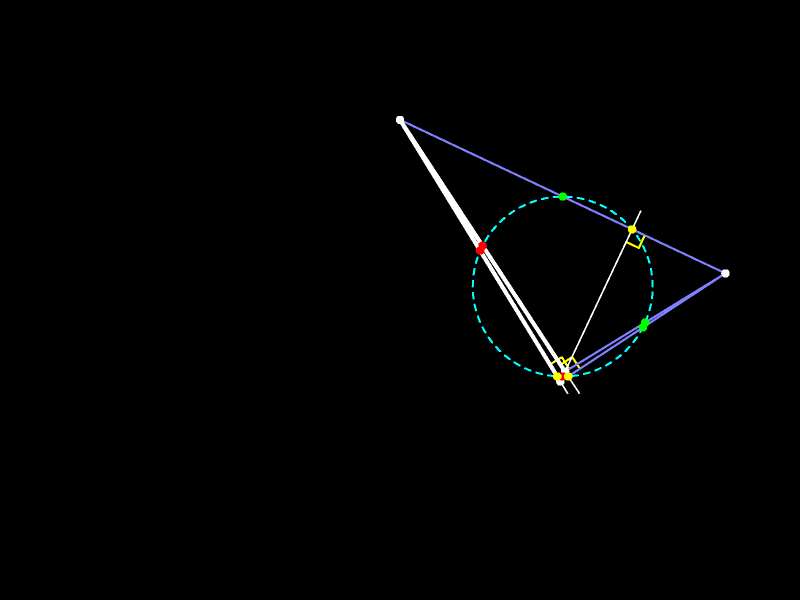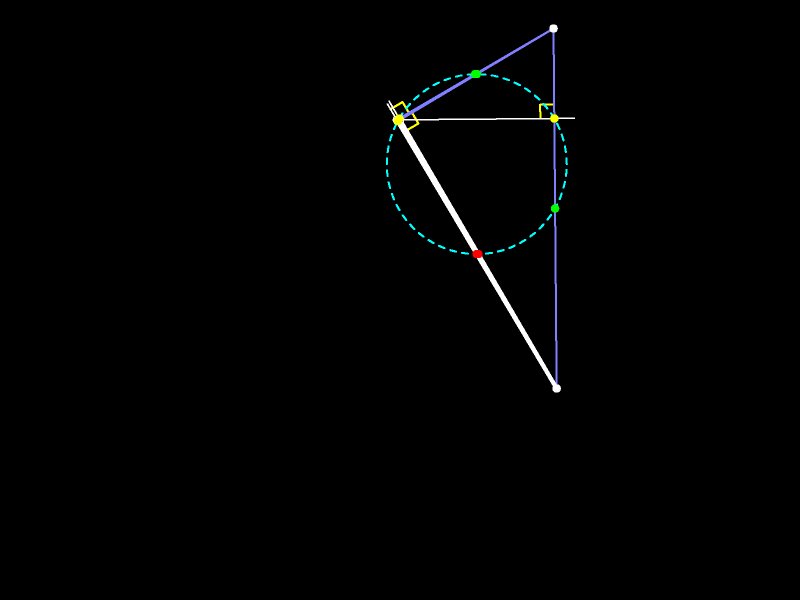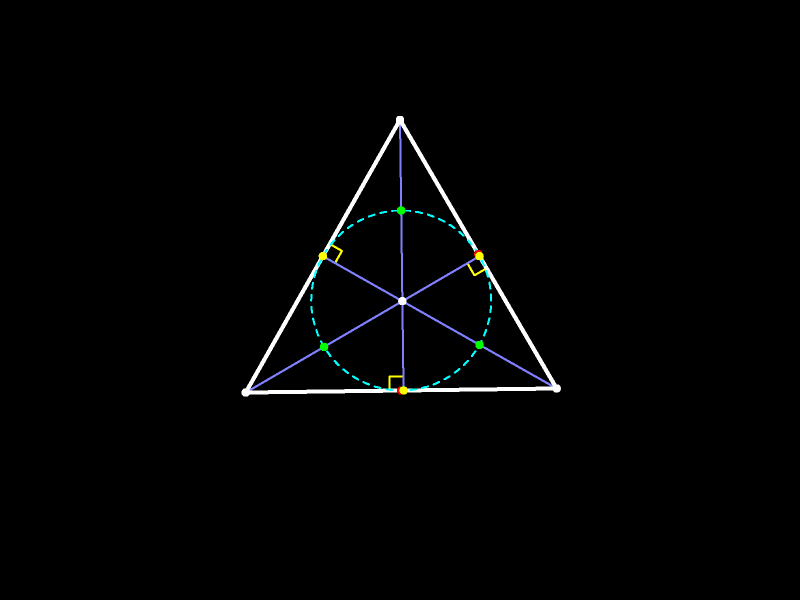
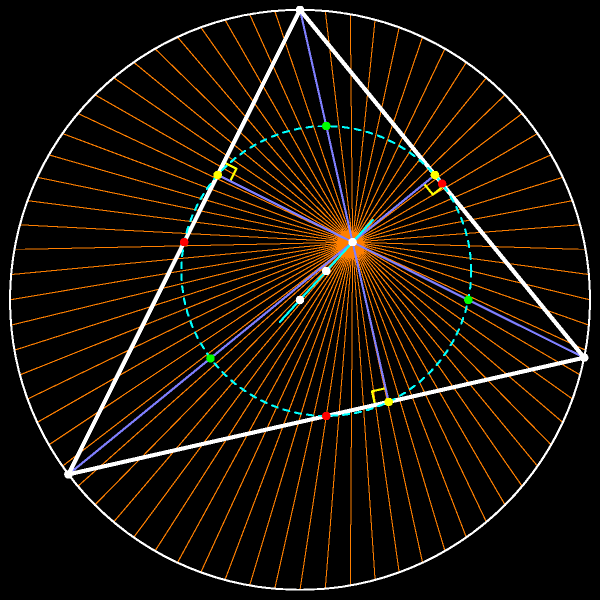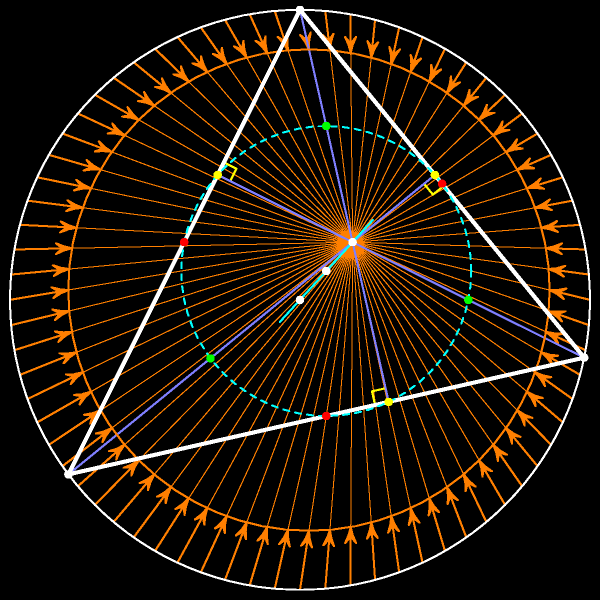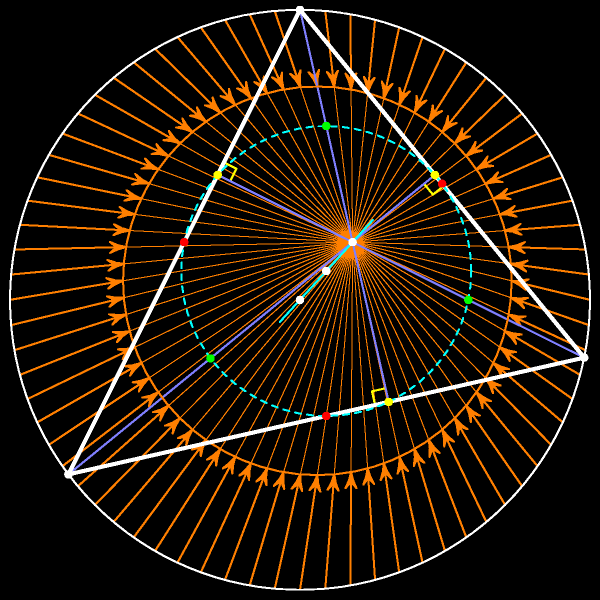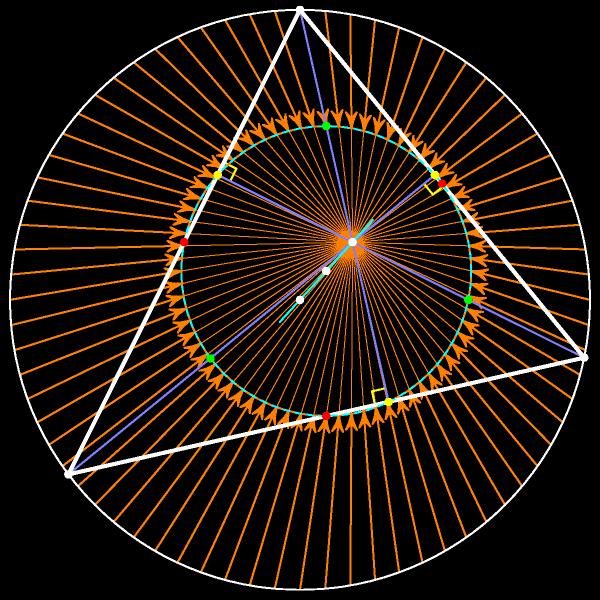 При гомотетии с центром в ортоцентре треугольника и
При гомотетии с центром в ортоцентре треугольника и
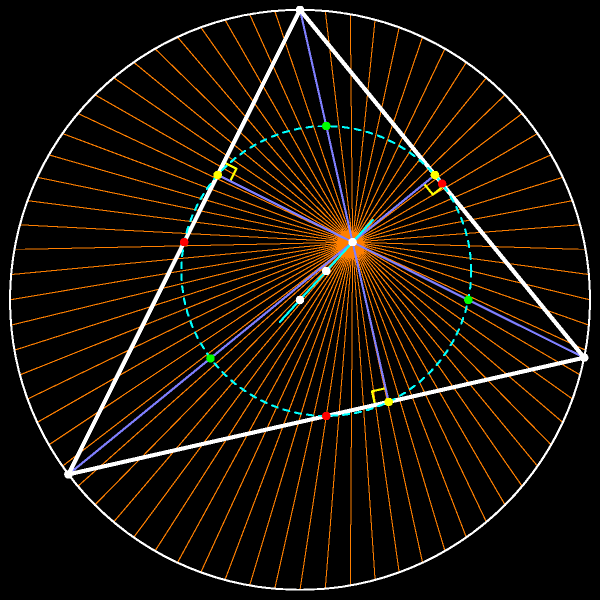 При этой гомотетии центр описанной окружности переходит в центр окружности девяти точек. Следовательно, центр окружности девяти
При этой гомотетии центр описанной окружности переходит в центр окружности девяти точек. Следовательно, центр окружности девяти
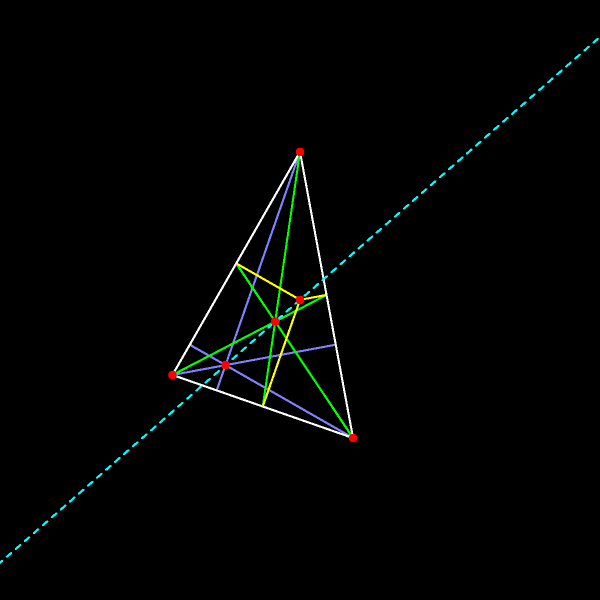 При гомотетии с центром в точке пересечения медиан и
При гомотетии с центром в точке пересечения медиан и
Таким образом, центр описанной окружности, центр тяжести, центр окружности девяти точек и ортоцентр лежат на одной
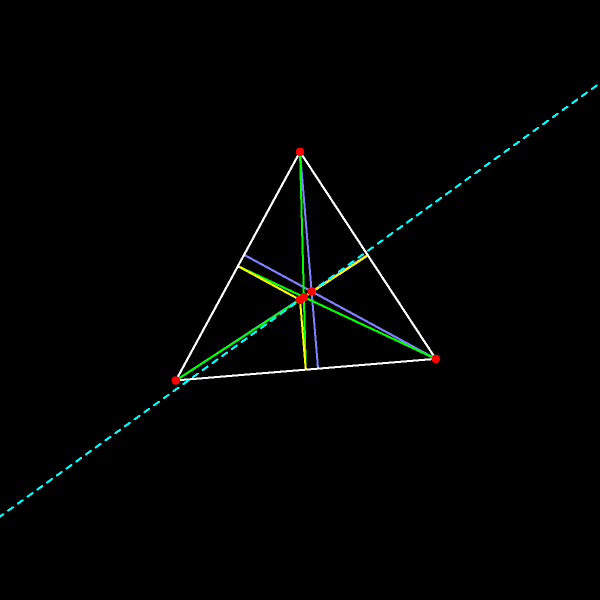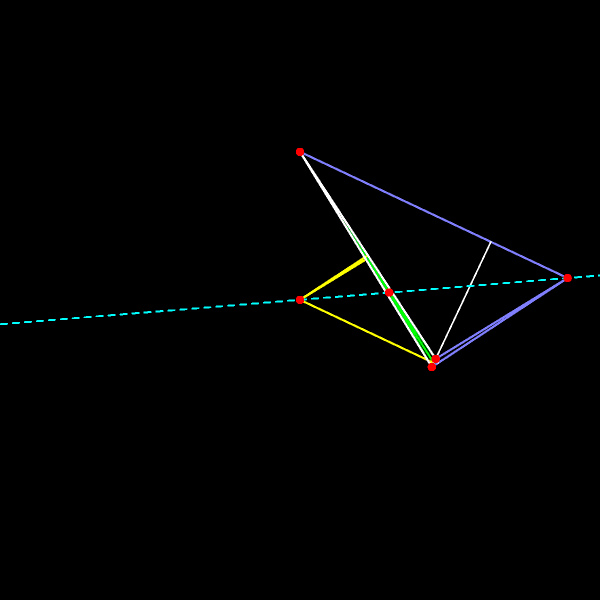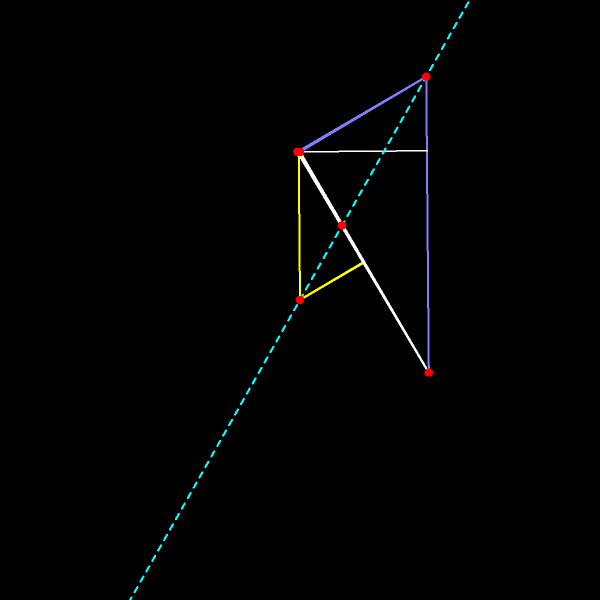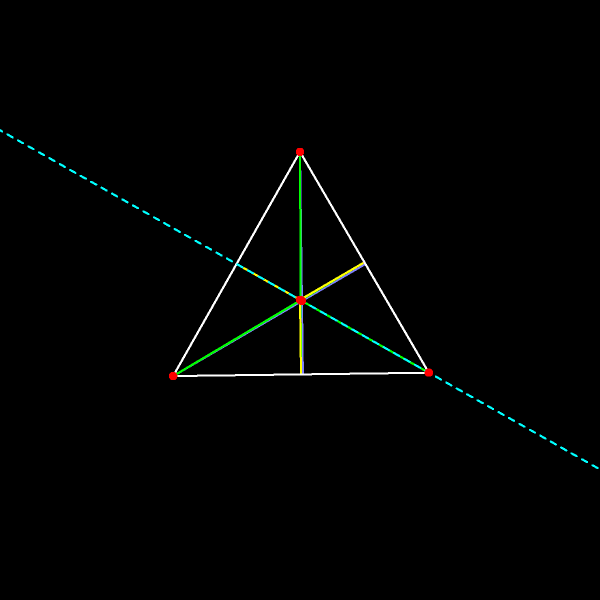 Вот как меняется прямая Эйлера при движении вершин треугольника.
Вот как меняется прямая Эйлера при движении вершин треугольника.
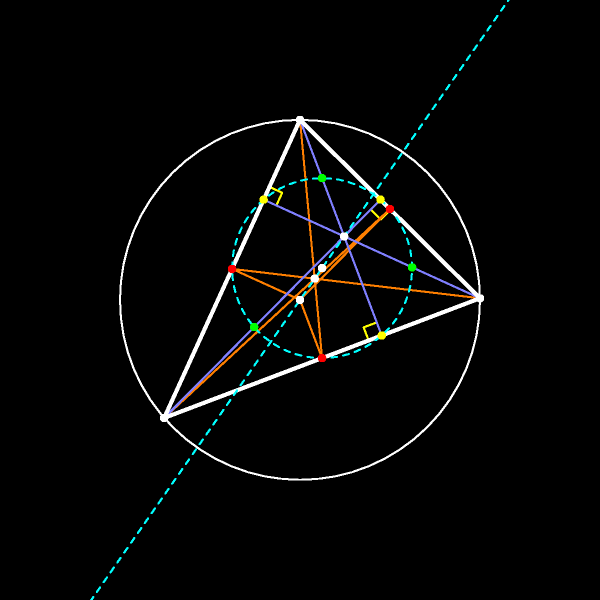 А вот так выглядят прямая Эйлера и окружность девяти точек, изображённые на одном рисунке.
А вот так выглядят прямая Эйлера и окружность девяти точек, изображённые на одном рисунке.
И, наконец, мультфильм!