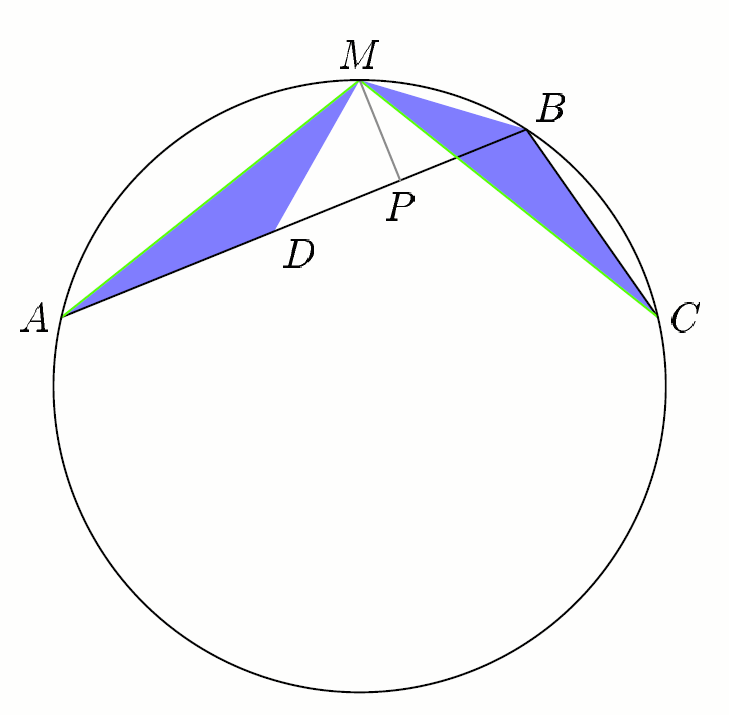
Задача Архимеда

Пусть треугольник ABC вписан в окружность, причём AB > BC; M — середина дуги AC, расположенная с той же стороны от прямой AC, что и точка B. Докажем, что основание P перпендикуляра, опущенного на отрезок AB из точки M, делит ломаную ABC пополам, то есть AP = PB + BC.

В силу теоремы о вписанном угле величины углов MAB и MCB, опирающихся на одну и ту же дугу MB, равны. Поэтому при повороте треугольника MCB вокруг точки M, при котором точка C переходит в точку A, треугольник MBC переходит в некоторый треугольник MDA, где точка D лежит на отрезке AB. При этом MB = MD. Поскольку высота равнобедренного треугольника является и его медианой, то DP = PB, что и требовалось доказать.

Эту задачу Архимеда Николай Борисович Васильев под «круглым» номером 1000 включил в задачник «Кванта», чтобы подчеркнуть неувядающую красоту древней геометрической задачи. Предложенное здесь решение придумала в 2006 году девятиклассница Эмма Акопян.