Площадь сегмента параболы

Рассмотрим произвольную параболу.

Две её произвольные точки соединим отрезком.

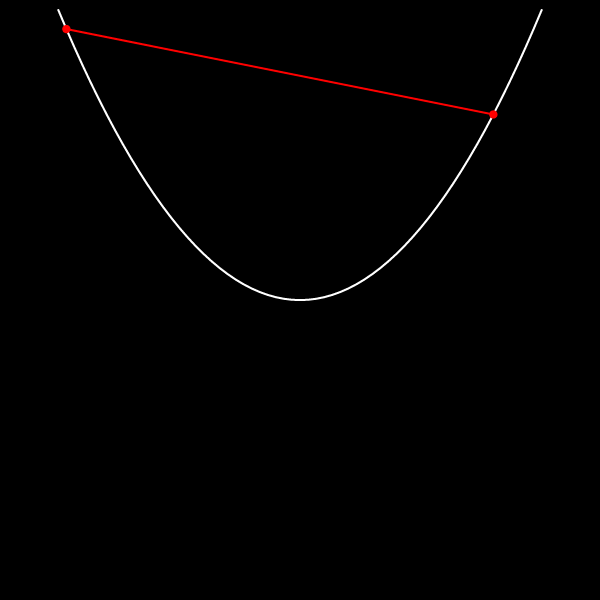
Часть плоскости, ограниченную этим отрезком и дугой параболы, называем сегментом параболы.

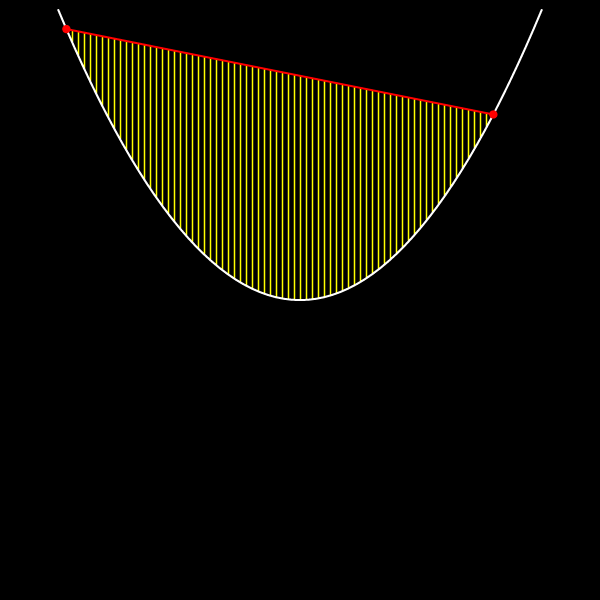
Через концы рассматриваемого отрезка проведём касательные к параболе. Архимед доказал, что площадь сегмента равна удвоенной площади части плоскости, образованной этими касательными и дугой параболы.

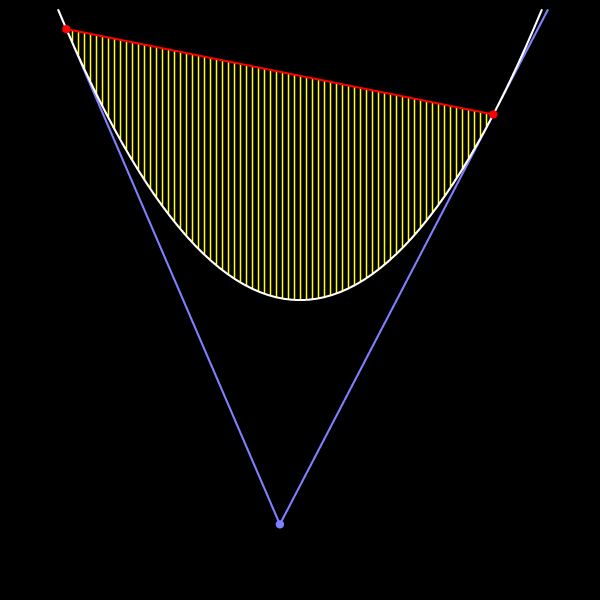
Доказательство основано на удивительно простом свойстве взаимного расположения параболы и треугольника, образованного касательными и хордой.

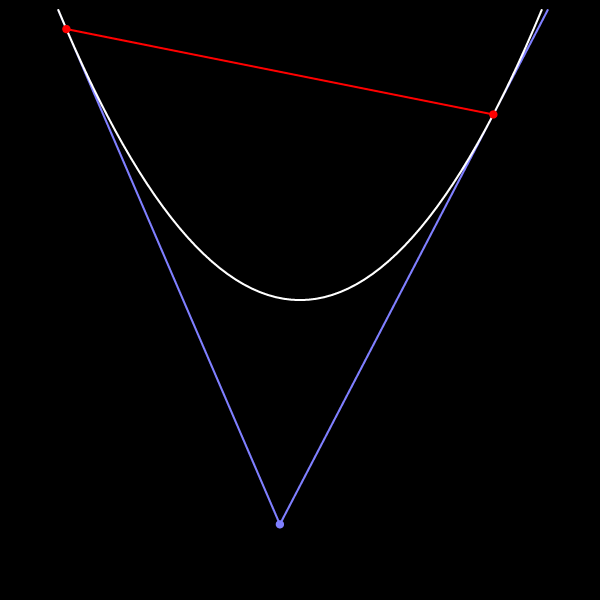
А именно, проведём среднюю линию этого треугольника, параллельную хорде параболы.

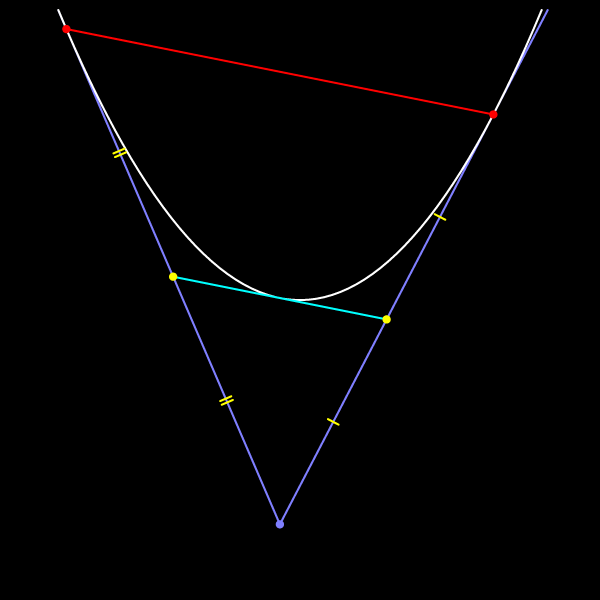
Она касается параболы! Это несложно доказать при помощи метода координат. Уравнения касательных к параболе, заданной уравнением y = ax², проходящих через точки B(b; ab²) и C(c; ac²) соответственно, легко найти: y = 2abx – ab² и y = 2acx – ac² соответственно. Решая уравнение 2abx – ab² = 2abx – ab², находим 2x = b + c и, следовательно, ордината точки A равна bc(b + c) – ab² = abc. Таким образом, абсцисса точки A пересечения касательных — среднее арифметическое чисел b и c, а ордината равна произведению abc.

Угловой коэффициент прямой BC равен частному от деления разности ординат (ac² – ab²) точек C и B на разность (c – b) их абсцисс, то есть числу a(b + c). Прямая BC задана уравнением y = a(b + c)x – abc, а параллельная ей прямая, проходящая через точку A, задана уравнением y = a(b + c)x – a((b² + c²) / 2). Правую часть уравнения средней линии треугольника ABC, параллельной прямой BC, получаем как среднее арифметическое правых частей уравнений, задающих прямую BC и паралельную ей прямую, проходящую через точку A. Таким образом, y = a(b + c)x – a((b + c) / 2)². Очевидно, мы получили уравнение прямой, касающейся параболы!

А можно было обойтись без вычислений: выбрав в качестве направления оси ординат направление оси симметрии параболы, ось сбсцисс направив параллельно прямой BC и выбрав начало координат так, чтобы оно совпало (в новой системе координат) с вершиной параболы, мы сводим дело к известному утверждению: касательная к параболе в любой её точке делит пополам отрезок между началом координат и проекцией на ось абсцисс точки, в которой проведена касательная.

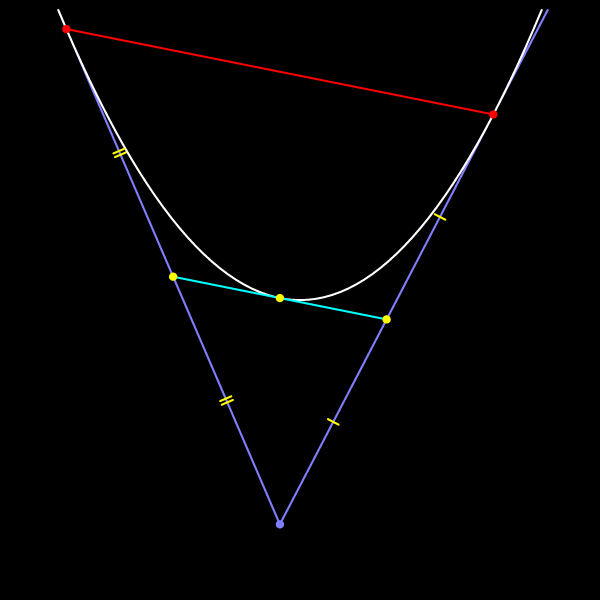
Из обоих способов доказательства следует, что точка касания делит среднюю линию треугольника пополам.

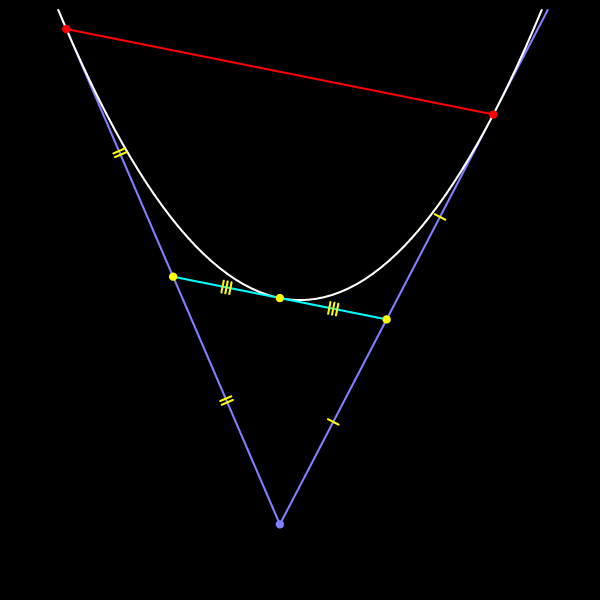
Средние линии любого треугольника делят его на четыре конгруэнтные части. Поэтому площадь любой из этих частей равна одной четвёртой части площади всего треугольника.

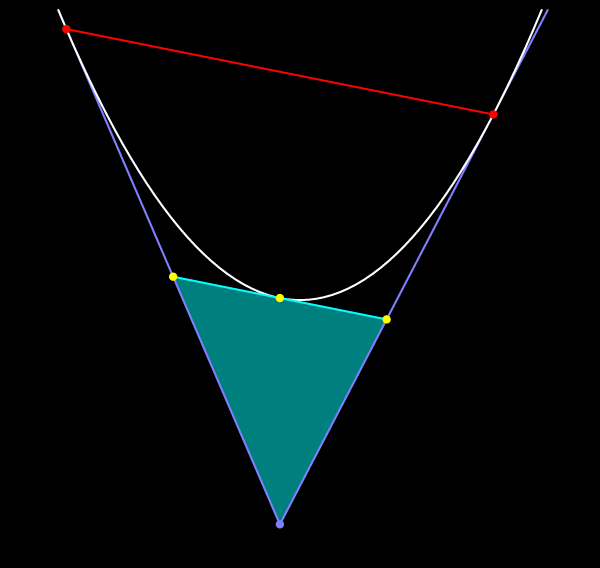
Повторим построение: проведём среднюю линию ещё одного треугольника, образованного хордой параболы и двумя касательными к ней. Площадь заштрихованного треугольника равна одной четвёртой части площади треугольника, среднюю линию которого мы только что провели.

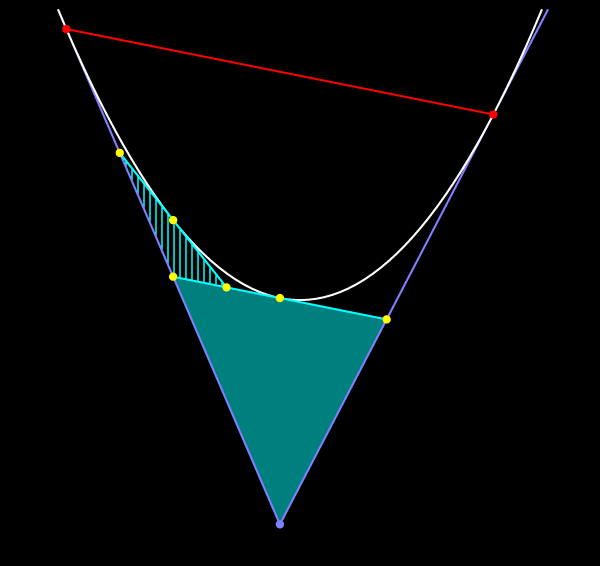
Площадь дважды заштрихованного треугольника равна одной восьмой части площади заштрихованного треугольника.

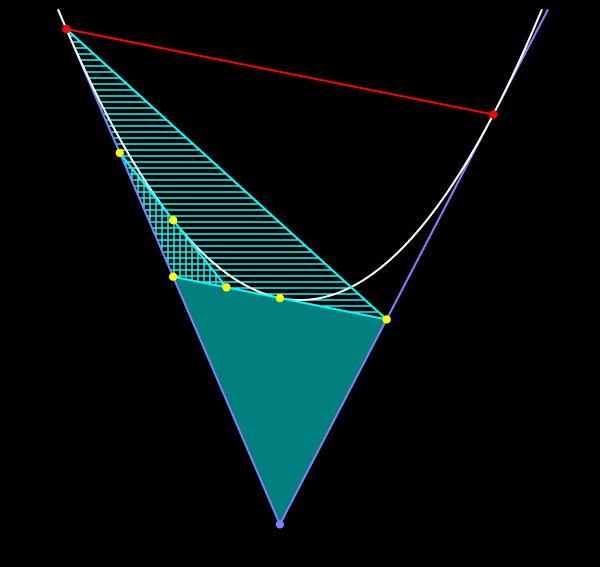
Поэтому его площадь равна одной тридцать второй части площади исходного треугольника.

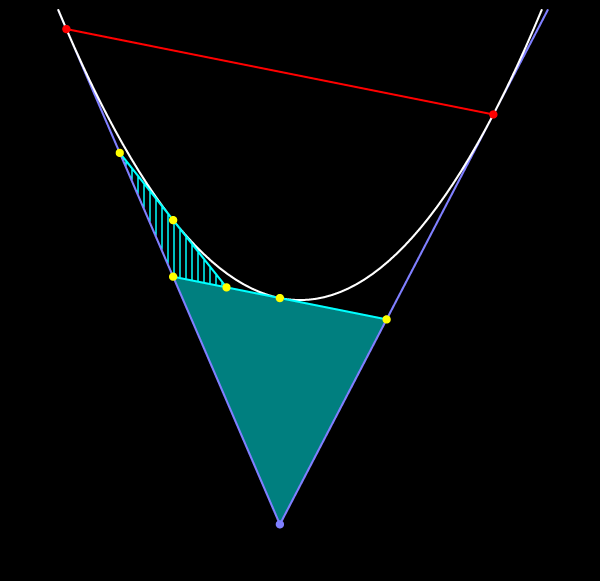
А в сумме со своим аналогом он составляет одну шестнадцатую часть площади исходного треугольника.

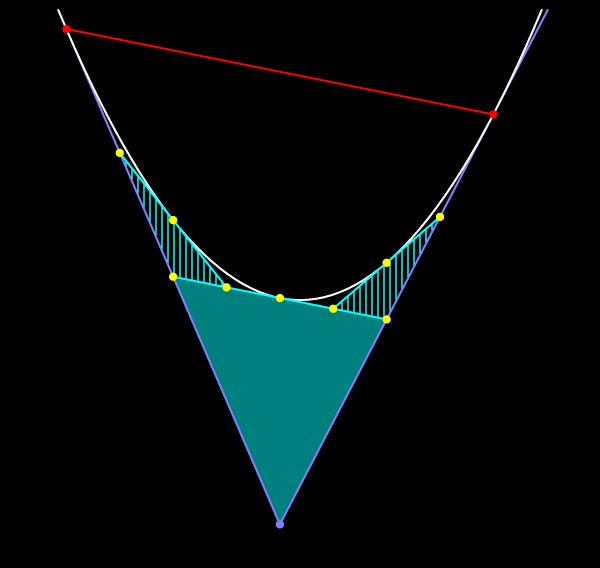
Такие построения можно продолжить: в каждом из четырёх треугольников, образованных касательными к параболе и её хордами, можно провести среднюю линию.

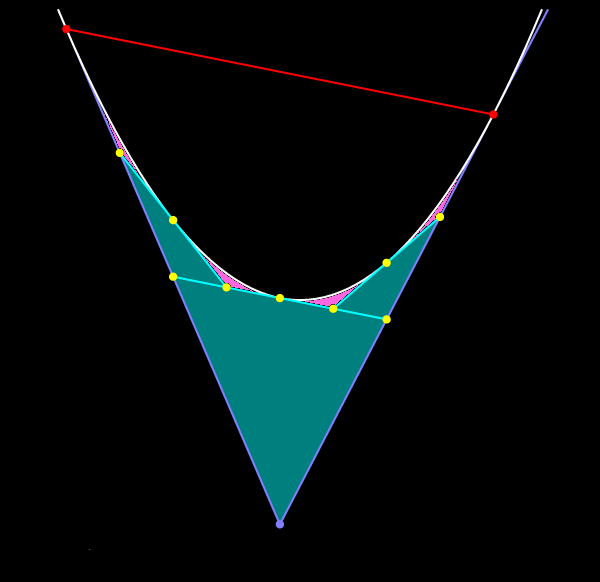
От исходного треугольника будут отрезаны 4 треугольника. (На рисунке показаны только точки касания проводимых средних линий: сами средние линии практически слились с параболой!) Для наших вычислений важно, что мы всякий раз будем отрезать вчетверо меньшую площадь, чем до этого.

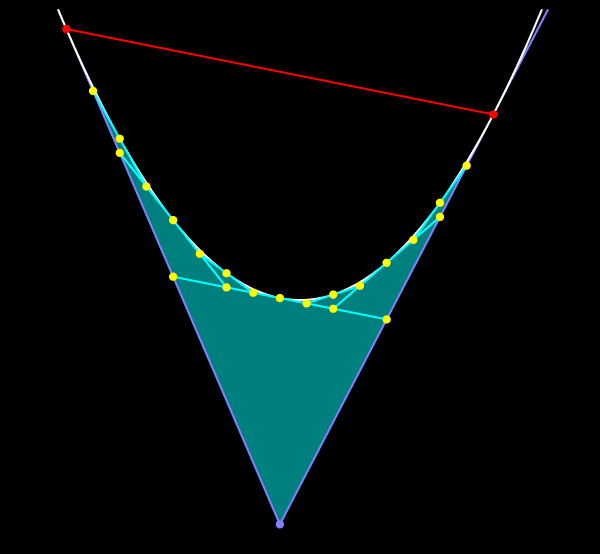
Таким образом, осталось вычислить сумму геометрической прогрессии с первым членом 1/4 и знаменателем 4.

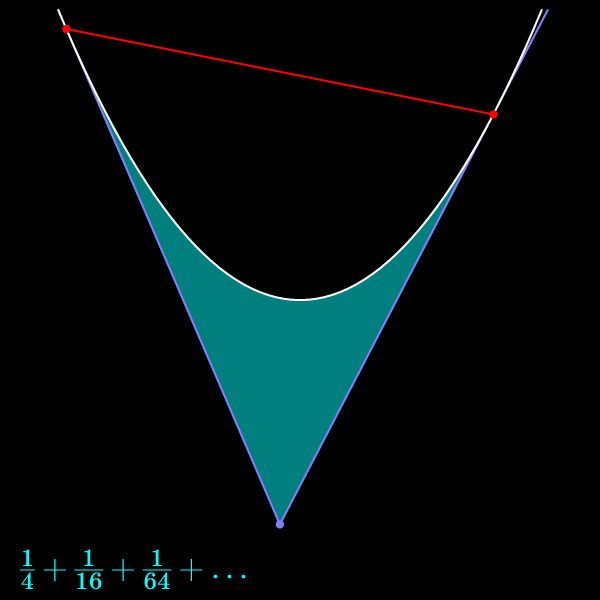
Обозначив сумму этой прогрессии буквой x и умножив все члены прогрессии на 4, получаем уравнение 4x = 1 + x.

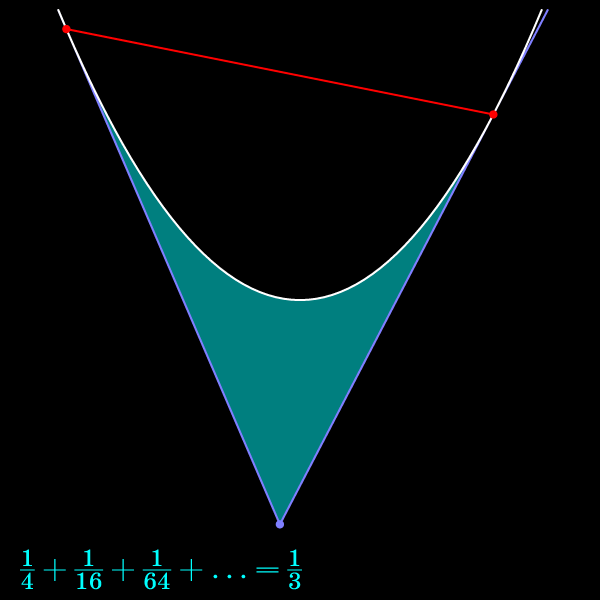
Решая уравнение, получаем ответ: x = 1/3.

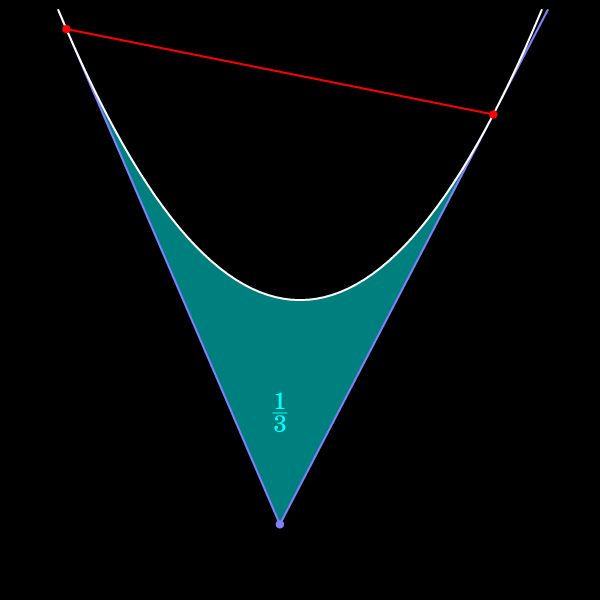
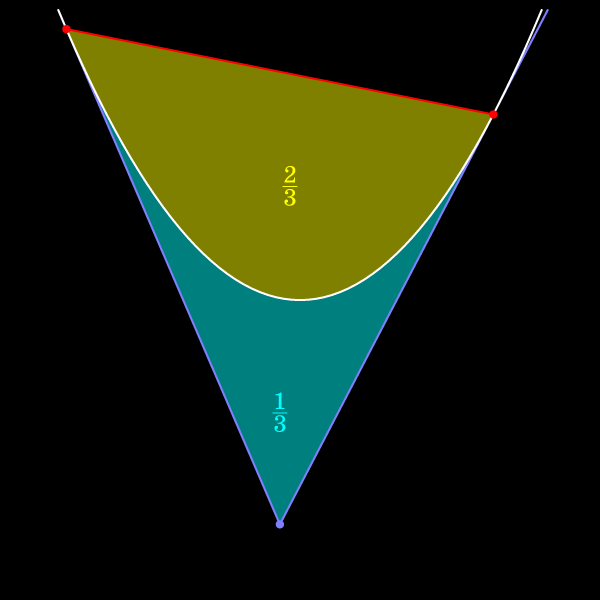
Площадь криволинейного треугольника, образованного касательными и дугой параболы, равна 1/3 площади треугольника. А остальная площадь — это площадь сегмента.

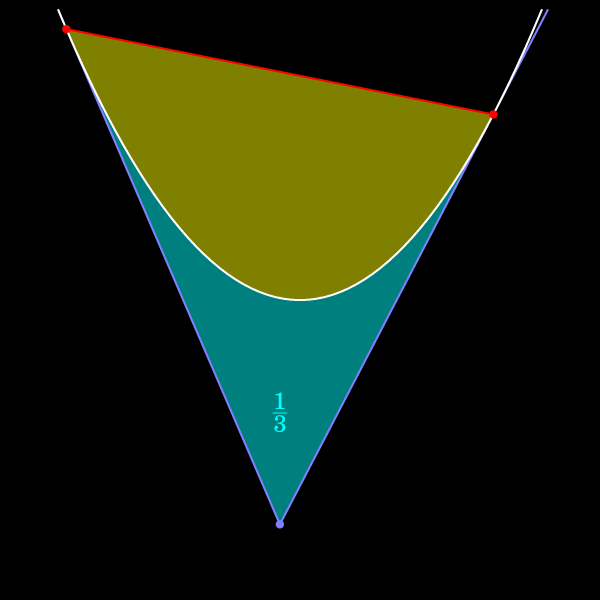
Таким образом, площадь сегмента равна 2/3 площади треугольника.