121. Для любых n вещественных чисел a₁, a₂, ..., a_n существует такое натуральное k £ n, что ни одно из чисел a_k, (a_k + a_k–1) ⁄ 2, (a_k + a_k–1 + a_k–2) ⁄ 3, ..., (a_k + a_k–1 + ... + a₂ + a₁) ⁄ k не превосходит среднего арифметического чисел a₁, a₂, ..., a_n.

122. Пятиугольник АВСDE вписан в окружность. Расстояния от точки Е до прямых АВ, ВС и СD равны соответственно p, q и r. Найдите расстояние от точки Е до прямой АD.

123*. Найдите все такие натуральные числа m, что произведение факториалов первых m нечётных натуральных чисел равно факториалу суммы первых m натуральных чисел.

124. а) Дан треугольник ABC. Найдите внутри него точку O, обладающую следующим свойством: для любой прямой, проходящей через точку O и пересекающей стороны AB и BC треугольника в точках K и L соответственно, сумма отношений AK ⁄ KB и CL ⁄ LB равна 1.

б) Если p и q — произвольно заданные положительные числа, то внутри треугольника ABC можно указать такую точку O, что для любой прямой KL, проходящей через эту точку (K лежит на AB, L — на BC), сумма выражений p · AK ⁄ KB и q · CL ⁄ LB равна 1. Докажите это.

125*. а) Существует ли бесконечная последовательность натуральных чисел, обладающая следующим свойством: ни одно из этих чисел не делится на другое, но среди каждых трёх чисел можно выбрать два, сумма которых делится на третье?

б) Если нет, то как много чисел может быть в наборе, обладающем таким свойством?

в) Решите ту же задачу при дополнительном условии: в набор разрешено включать только нечётные числа. (Вот пример такого набора из четырёх чисел: 3, 5, 7, 107. Здесь среди трёх чисел 3, 5, 7 сумма 5 + 7 делится на 3; в тройке 5, 7, 107 сумма 107 + 5 делится на 7; в тройке 3, 7, 107 сумма 7 + 107 делится на 3; наконец, в тройке 3, 5, 107 сумма 3 + 107 делится на 5.)

126. Многоугольник, описанный вокруг окружности радиусом r, разрезали на треугольники. Докажите, что сумма радиусов вписанных окружностей этих треугольников больше r.

127. Для каждого натурального n обозначим через s(n) сумму цифр его десятичной записи. Назовём натуральное число m особым, если его нельзя представить в виде m = n + s(n). Конечно или бесконечно множество особых чисел? (Например, число 117 не особое, поскольку 117 = 108 + s(108), а число 121, как нетрудно убедиться,— особое.)

128. Найдите отношение сторон треугольника, одна из медиан которого делится вписанной окружностью на три равные части.

129. а) В ведро налили 12 литров молока. Пользуясь лишь сосудами в 5 и 7 литров, разделите молоко на две равные части.

б) Решите общую задачу: при каких a и b можно разделить пополам (a + b) литров молока, пользуясь лишь сосудами в a литров, b литров и (a + b) литров?

За одно переливание из одного сосуда в другой можно вылить всё, что там есть, или долить второй сосуд до верха.

130. Какое наибольшее число точек можно разместить а) на плоскости; б*) в пространстве так, чтобы ни один из треугольников с вершинами в этих точках не был тупоугольным?

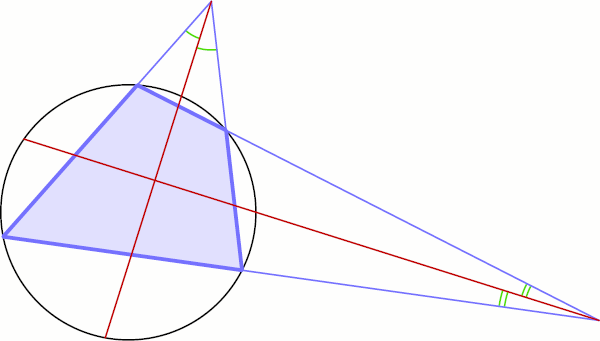131. Четыре точки, в которых биссектрисы углов между продолжениями противоположных сторон вписанного четырёхугольника пересекают его стороны, являются вершинами ромба. Докажите это.

132. По окружности выписаны n чисел x₁, x₂, ..., x_n, каждое из которых равно 1 или –1, причём сумма произведений соседних чисел равна нулю (как в задаче 93) и вообще для каждого k = 1, 2, ..., n – 1 сумма n произведений чисел, отстоящих друг от друга на k мест, равна нулю (то есть x₁x₃ + x₂x₄ + ... = 0, x₁x₄ + x₂x₅ + ... = 0 и так далее; например, для n = 4 можно взять одно из чисел равным –1, а три других — равными 1).

а) Докажите, что n — квадрат целого числа.

б) Существует ли такой набор чисел для n = 16? (Мы не знаем, при каких n такой набор чисел существует.)

133. Один из простейших многоклеточных организмов — водоросль вольвокс — представляет собой сферическую оболочку, сложенную, в основном, семиугольными, шестиугольными и пятиугольными клетками (то есть клетками, имеющими семь, шесть или пять соседних; в каждой «вершине» сходятся три клетки). Бывают экземпляры, у которых есть и четырёхугольные, и восьмиугольные клетки, но биологи заметили, что если таких «нестандартных» клеток (менее чем с пятью и более чем с семью сторонами) нет, то пятиугольных клеток на 12 больше, чем семиугольных (всего клеток может быть несколько сотен и даже тысяч). Объясните этот факт.

134. Какое множество точек заполняют центры тяжести треугольников, три вершины которых лежат соответственно на трёх сторонах АВ, ВС и АС данного треугольника АВС?

135*. Для каждого натурального n > 1 существует такое число c_n, что для любого x произведение синуса числа x, синуса числа x + ^π⁄_n, синуса числа x + ^2π⁄_n, ..., наконец, синуса числа x + ^{(n – 1)π}⁄_n равно произведению числа c_n на синус числа nx. Докажите это и найдите величину c_n.

136. Можно ли увезти из каменоломни 50 камней, массы которых 370 кг, 372 кг, 374 кг, ..., 468 кг (массы составляют арифметическую прогрессию с разностью 2 кг), на семи трёхтонках?

137. a, b, c, d — длины четырёх последовательных сторон четырёхугольника, S — его площадь. Докажите неравенства: а) S £ ab + cd; б) S £ ac + bd.

в) Если хотя бы в одном из этих неравенств достигается равенство, то четырёхугольник можно вписать в окружность. Докажите это.

138. Если m и n — натуральные числа, причём m < n, то сумма чисел вида (–1)^kk^mС^k_n, где k пробегает значения от 1 до n, равна нулю. Докажите это.

Здесь С^k_n — это коэффициент при x^k после раскрытия скобок и приведения подобных в многочлене (1 + x)ⁿ. Например, если n = 4, то C⁰₄ = 1, C¹₄ = 4, C²₄ = 6, C³₄ = 4, C⁴₄ = 1 и верны равенства

139. Из вершины B параллелограмма ABCD проведены его высоты BK и BH. Выразите расстояние от точки В до точки пересечения высот треугольника ВKН через длины отрезков KH = a и BD = b.

140. С натуральным числом (записываемым в десятичной системе) разрешено проделывать следующие операции:

А) приписать на конце цифру 4;

Б) приписать на конце цифру 0;

В) разделить на 2 (если число чётно).

Например, если с числом 4 проделаем последовательно операции В, В, А и Б, то получим число 140.

а) Из числа 4 получите число 1972.

б*) Из числа 4 можно получить любое натуральное число. Докажите это.

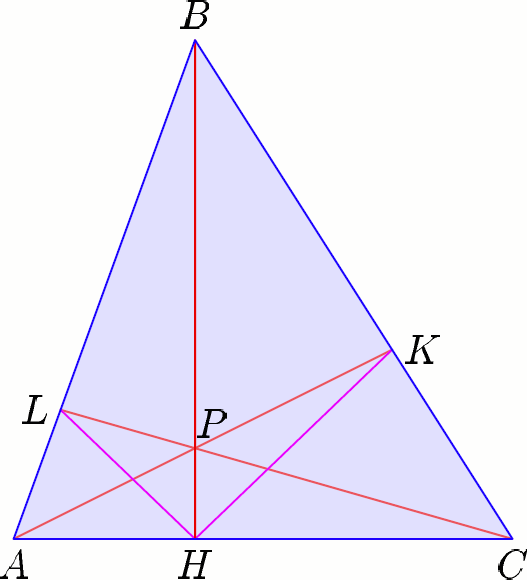141. Выберем на высоте ВН треугольника АВС произвольную точку Р. Пусть K — точка пересечения прямых АР и ВС, L — точка пересечения прямых СР и АВ. Докажите, что отрезки KН и LН составляют равные углы с высотой ВН.

142. а) Нельзя занумеровать рёбра куба числами 1, 2, ..., 11, 12 так, чтобы для каждой вершины сумма номеров трёх выходящих из неё рёбер была одной и той же. Докажите это.

б*) Можно ли вычеркнуть одно из чисел 1, 2, ..., 12, 13 и оставшимися занумеровать рёбра куба так, чтобы выполнялось то же условие?

143. Найдите наименьшее натуральное число n, для которого выполнено следующее условие: если число p простое и n делится на (p – 1), то n делится на p.

144*. Найдите необходимые и достаточные условия, которым должны удовлетворять числа a, b, α и β, чтобы прямоугольник размером a×b можно было разрезать на прямоугольники размером α×β. Например, можно ли прямоугольник размером 50×60 разрезать на прямоугольники размером а) 20×15; б) 5×8; в) 6,25×15; г) (2 + d)×(2 – d), где буква d обозначает длину диагонали квадрата со стороной 1?

145. Хозяин обещает работнику платить в среднем корень из двух рублей в день. Для этого каждый день он платит 1 или 2 рубля с таким расчётом, чтобы для любого натурального n выплаченная за первые n дней сумма была натуральным числом, наиболее близким к произведению корня из двух и числа n. Вот величины первых пяти выплат: 1, 2, 1, 2, 1. Докажите, что последовательность выплат непериодическая.

146. а) В вершинах правильного 7-угольника расставлены чёрные и белые фишки. Докажите, что найдутся 3 фишки одного цвета, лежащие в вершинах равнобедренного треугольника.

б) Верно ли аналогичное утверждение для 8-угольника?

в) Для каких правильных n-угольников аналогичное верно, а для каких — нет?

147. Вписанный в окружность четырёхугольник ABCD таков, что касательные к окружности в точках А и C пересекаются на продолжении диагонали ВD. Докажите, что

а) касательные в точках В и D пересекаются на продолжении диагонали АС;

б) биссектрисы внутренних углов А и C четырёхугольника пересекаются на диагонали ВD, а биссектрисы углов В и D — на АС.

148. Последовательность x₀, x₁, x₂, ... определена следующими условиями: x₀ = 1, x₁ = λ, для любого n > 1 выполнено равенство

Здесь α, β, λ — заданные положительные числа. Найдите x_n и выясните, при каком n величина x_n наибольшая.

149. Пусть O — точка пересечения диагоналей четырёхугольника АВCD. Докажите, что если равны периметры треугольников

а) ABC, BCD, CDA и DAB, то АВCD — прямоугольник;

б) АBО, BCO, CDO и DAO, то АВCD — ромб.

150*. P и Q — подмножества множества выражений вида (a₁, a₂, ..., a_n), где a₁, a₂, ..., a_n — натуральные числа, не превосходящие данного числа k (очевидно, таких выражений всего kⁿ штук). Для любого элемента (p₁, p₂, ..., p_n) множества P и любого элемента (q₁, q₂, ..., q_n) множества Q существует хотя бы одно такое число m, что 1 £ m £ n и p_m = q_m. Докажите, что хотя бы одно из множеств P и Q состоит не более чем из k^{n – 1} элементов для

а) k = 2 и любого натурального n;

б) n = 1, 2 или 3 и любого натурального k >1;

в) произвольного натурального n и произвольного не равного 1 натурального числа k.

151. Каждая из девяти прямых разбивает квадрат на два четырёхугольника, площади которых относятся как 2 : 3. Докажите, что по крайней мере три из этих девяти прямых проходят через одну точку.

152. Пусть a, b, m, n — натуральные числа, причём числа a и b взаимно просты и a > 1. Докажите, что если a^m + b^m делится на aⁿ + bⁿ, то m делится на n.

153*. Двое играют в следующую игру. Один называет цифру, а другой вставляет её по своему усмотрению вместо одной из звёздочек в следующей разности: **** – ****. Затем первый называет ещё одну цифру, второй ставит её, первый опять называет цифру, и так играют до тех пор, когда все звёздочки будут заменены цифрами. Первый стремится к тому, чтобы разность получилась как можно больше, а второй — чтобы она стала как можно меньше. Докажите, что

а) второй может расставлять цифры так, чтобы модуль полученной разности стал не больше 4000, независимо от того, какие цифры называл первый;

б) первый может называть цифры так, чтобы модуль разности стал не меньше 4000, независимо от того, куда расставляет цифры второй.

154. На прямой дано 50 отрезков. Докажите, что верно хотя бы одно из следующих утверждений:

• некоторые 8 из этих отрезков имеют общую точку;
• некоторые 8 из этих отрезков таковы, что никакие два из них не пересекаются.

155*. Дано несколько квадратов, сумма площадей которых равна 1. Докажите, что их можно поместить без наложений в квадрат площади 2.

156. Точки M и N — середины сторон AD и BC прямоугольника ABCD. На продолжении отрезка DC за точку D лежит точка P. Прямые PM и AC пересекаются в точке Q. Докажите равенство углов QNM и MNP.

157. Сумма n положительных чисел x₁, x₂, x₃, ..., x_n равна 1. Пусть S — наибольшее из чисел x₁/(1 + x₁), x₂/(1 + x₁ + x₂), ..., x_n/(1 + x₁ + x₂ + ... + x_n). Найдите наименьшее возможное значение S. При каких значениях x₁, x₂, x₃, ..., x_n оно достигается?

158. Треугольная таблица строится по следующему правилу: в верхней её строке написано одно только натуральное число a > 1, а далее под каждым числом k слева пишем число k² , а справа — число k + 1. Докажите, что в каждой строке таблицы все числа разные. (Например, при a = 2 вторая строка состоит из чисел 4 и 3, третья — из чисел 16, 5, 9 и 4, четвёртая — из чисел 256, 17, 25, 6, 81, 10, 16 и 5.)

159*. Можно ли расставить цифры 0, 1 и 2 в клетках листа клетчатой бумаги размером 100×100 таким образом, чтобы в каждом прямоугольнике размером 3×4, стороны которого идут по сторонам клеток, были бы три нуля, четыре единицы и пять двоек?

160*. Когда закончился хоккейный турнир (в один круг), оказалось, что для любой группы команд можно найти команду (может быть, из той же группы), которая набрала в играх с командами этой группы нечётное число очков. Докажите, что в турнире участвовало чётное число команд. (Поражение — 0 очков, ничья — 1 очко, выигрыш — 2 очка.)

161. Озеро имеет форму невыпуклого n-угольника. Докажите, что множество точек озера, из которых видны все его берега, либо пусто, либо является внутренностью некоторого выпуклого m-угольника, где m £ n.

162. Последовательность натуральных чисел a₁ < a₂ < a₃ < ... < a_n < ... такова, что каждое натуральное число либо входит в последовательность, либо представимо в виде суммы двух членов последовательности, быть может, одинаковых. Докажите неравенство a_n £ n² для любого n = 1, 2, 3, ...

163. Если диагонали четырёхугольника перпендикулярны, то проекции их точки пересечения на стороны (или их продолжения) лежат на одной окружности. Докажите это.

164. На белых клетках бесконечной шахматной доски, заполняющей верхнюю полуплоскость, записаны какие-то числа так, что для каждой чёрной клетки сумма чисел, стоящих в двух соседних с ней клетках — справа и слева,— равна сумме двух других чисел, стоящих в соседних с ней клетках — сверху и снизу. Известно число, стоящее в одной клетке n-й строки (голубой крестик на рисунке), а требуется узнать число, стоящее над ним в (n + 2)-й строке (красный знак вопроса на рисунке). Сколько ещё чисел, стоящих в двух нижних строках (голубые точки на рисунке), нужно для этого знать?

165*. На окружности расположено множество F точек, состоящее из 100 дуг. При любом повороте R окружности множество R(F) имеет хотя бы одну общую точку с множеством F. (Другими словами, для любого угла α от 0° до 180° в множестве F можно указать две точки, отстоящие одна от другой на угол α.) Какую наименьшую сумму длин могут иметь 100 дуг, образующих множество F? Каков будет ответ, если дуг не 100, а n?

166. а) Школьники одного класса в сентябре ходили в два туристических похода. В первом походе мальчиков было меньше ²⁄₅ общего числа участников этого похода, во втором — тоже меньше ²⁄₅. Докажите, что в этом классе мальчики составляют меньше ⁴⁄₇ общего числа учеников, если известно, что каждый из учеников участвовал по крайней мере в одном походе.

б) Пусть в k-м походе, где 1 £ k £ n, мальчики составляли α_k-ю часть общего количества участников этого похода. Какую наибольшую долю могут составлять мальчики на общей встрече всех туристов (всех, кто участвовал хотя бы в одном из n походов)?

167. В любой арифметической прогрессии a, a + d, a + 2d, ..., a + nd, ..., составленной из натуральных чисел, есть бесконечно много членов, в разложении которых на простые множители входят в точности одни и те же простые числа. Докажите это.

168. В правильной усечённой пирамиде точка K — середина некоторой стороны АВ верхнего основания, L — середина некоторой стороны CD нижнего основания. Докажите равенство длин проекций отрезков АВ и CD на прямую KL.

169. k и n — натуральные числа, k £ n. Расставьте первые n² натуральных чисел в таблицу n×n так, чтобы в каждой строке числа шли в порядке возрастания и при этом сумма чисел в k-м столбце была а) наименьшей; б) наибольшей.

170. а) M и N — точки касания вписанной в треугольник АВС окружности со сторонами АВ и АС, Р — точка пересечения прямой MN с биссектрисой угла В. Докажите, что угол BPC прямой.

б) Докажите более общий факт: если расположенная внутри треугольника ABC точка O такова, что величина угла BOC на 90° больше величины угла BAO, точки M и N — основания перпендикуляров, опущенных из точки O на стороны AB и AC, а P — точка пересечения прямых BO и MN, то угол BPC прямой.

171. На плоскости нарисован правильный шестиугольник, длина стороны которого равна 1. При помощи одной только линейки постройте отрезок, длина которого равна квадратному корню из 7.

172. Пусть p — простое число. Напишем сначала p единиц, затем p двоек, p троек, p четвёрок, p пятёрок, p шестёрок, p семёрок, p восьмёрок и p девяток. Докажите, что полученное таким образом число при делении на p даёт такой же остаток, что и число 123 456 789.

173*. В квадратной таблице 4×4 расставлены числа 1, 2, 3,..., 16 так, что сумма четырёх чисел в каждой строке, в каждом столбце и на каждой из двух диагоналей равна одному и тому же числу, причём числа 1 и 16 стоят в противоположных углах таблицы. Докажите, что в этом «магическом квадрате» сумма любых двух чисел, расположенных симметрично относительно центра квадрата, одна и та же.

174. На сторонах треугольника ABC, как на основаниях, построены равнобедренные треугольники AB₁C, BA₁C и AC₁B. Докажите, что перпендикуляры, опущенные из точек A, B и C соответственно на прямые B₁C₁, C₁A₁ и A₁B₁, пересекаются в одной точке.

175*. Найдите для каждого данного натурального числа m такое наибольшее возможное число N, что возможна следующая ситуация.

а) Каждая сторона равностороннего треугольника разбита на m равных частей; через точки деления проведены прямые, параллельные сторонам и разрезавшие треугольник на m² маленьких треугольников. Среди вершин полученных треугольников отмечены N вершин так, что ни для каких двух отмеченных вершин A и B отрезок АВ не параллелен ни одной из сторон (на рисунке m = 6).

б) Каждое ребро тетраэдра разделено на m равных частей; через точки деления проведены плоскости, параллельные граням. Среди вершин полученных многогранников отмечены N вершин так, чтобы никакие две отмеченные вершины не лежат на прямой, параллельной одной из граней.

в) Среди решений уравнения x₁ + x₂ + ... + x_k = m в целых неотрицательных числах выбраны N решений так, что ни в каких двух из выбранных решений ни одна переменная не принимает одно и то же значения.

Примечание. Задачи а) и б) являются частными случаями задачи в) при k = 2 и k = 3 соответственно.

176. К какой стороне треугольника ABC ближе всего расположена точка пересечения его высот, если РA < РB < РC? А к какой вершине?

177. Пусть a — заданное вещественное число, n — натуральное число, n > 1. Найдите все такие x, что сумма корней n-й степени из чисел xⁿ – aⁿ и 2aⁿ – xⁿ равна числу a.

178. Из некоторой точки P биссектрисы угла A треугольника ABC опустим перпендикуляры PA₁, PB₁ и PC₁ на его стороны BC, CA и AB соответственно. Пусть R — точка пересечения прямых PA₁ и B₁C₁. Докажите, что прямая АR делит сторону ВС пополам.

179*. Для каждого непрямоугольного треугольника T обозначим через T₁ треугольник, вершинами которого служат основания высот треугольника T; через T₂ — треугольник, вершинами которого служат основания высот треугольника T₁; аналогично определим треугольники T₃, T₄ и так далее. Каким должен быть треугольник T, чтобы а) треугольник T₁ был остроугольным? б) в последовательности T₁, T₂, T₃,... встретился прямоугольный треугольник T_n (и таким образом треугольник T_n+1 не был определён)? в) треугольник T₃ был подобен треугольнику T?

г) Для каждого натурального числа n выясните, сколько существует неподобных другу треугольников T, для которых треугольник T_n подобен треугольнику Т.

180*. Двое играют в такую игру. Один задумывает натуральное число n, а другой задаёт вопросы типа «верно ли, что n не меньше x?» (число x он может выбирать по своему усмотрению) и получает ответы «да» или «нет». Каждой возможной стратегии T второго игрока сопоставим функцию f_T(n), равную числу вопросов (до отгадывания), если было задумано число n. Пусть, например, стратегия T состоит в том, что сначала задают вопросы: «верно ли, что n не меньше 10?», «верно ли, что n не меньше 20?», ... до тех пор, пока на какой-то вопрос «верно ли, что n не меньше 10(k + 1)?» не будет дан ответ «нет», а затем задают вопросы «верно ли, что n не меньше 10k + 1?», «верно ли, что n не меньше 10k + 2?» и так далее. Тогда f_T(n) = a + 2 + ^{(n – a)}⁄₁₀, где a — последняя цифра числа n, то есть f_T(n) растёт примерно как ⁿ⁄₁₀.

а) Предложите стратегию, для которой функция f_T растёт медленнее.

б) Сравнивая две стратегии, удобно для произвольной стратегии Т вместо функции f_T ввести функцию f_T, значение которой для любого натурального числа n равно наибольшему из чисел f_T(k), где k пробегает значения от 1 до n. Оцените снизу f_T для произвольной стратегии T.