361. Двое играют в следующую игру. Сначала на клетчатой бумаге выделяют прямоугольник размером m×n клеток. Ходят по очереди. Каждым ходом игрок вычёркивает все клетки какого-то горизонтального или вертикального ряда, в котором ещё остались невычеркнутые клетки. Побеждает тот, кто делает последний ход, то есть вычёркивает последние клетки. Кто может обеспечить себе выигрыш: начинающий или его партнёр? (Ответ, конечно, зависит от m и n).

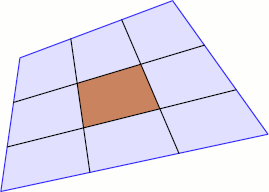362. Разделим каждую сторону выпуклого четырёхугольника ABCD на три равные части и соединим отрезками соответствующие точки на противоположных сторонах. Докажите, что площадь «среднего» четырёхугольника в 9 раз меньше площади четырёхугольника ABCD.

363. Две параболы с параллельными осями пересекаются в точках A₀ и B₀. На первой параболе взяты точки A₁, A₂, ..., A_2n, а на второй — точки B₁, B₂, ..., B_2n так, что прямая A_kA_k+1 параллельна прямой B_kB_k+1 для любого целого неотрицательного числа k < 2n. Докажите, что прямая A₀B_2n параллельна прямой B₀A_2n.

364. Из 16 космонавтов нужно выбрать 4-х — экипаж космического корабля. Тренировки проводятся с 4-мя экипажами по 4 человека в каждом. Можно ли составить расписание тренировок таким образом, чтобы любые два космонавта побывали в одном экипаже ровно один раз?

365. а) Сумма нескольких чисел равна единице. Может ли сумма их кубов быть больше единицы?

б) Тот же вопрос для чисел, каждое из которых меньше единицы.

в) Может ли случиться, что некоторый ряд a₁ + a₂ + a₃ + ... сходится, а ряд a₁³ + a₂³ + a₃³ + ..., образованный кубами его членов, расходится?

Ряд x₁ + x₂ + x₃ + ... называют сходящимся, если последовательность его частичных сумм S_n = x₁ + x₂ + ... + x_n стремится к некоторому конечному пределу.

366. Можно ли расположить на плоскости несколько треугольников так, чтобы две вершины каждого из них лежали на сторонах (но не в вершинах) других треугольников?

367. Может ли произведение а) трёх; б) четырёх последовательных натуральных чисел равняться некоторой степени некоторого натурального числа (квадрату, кубу, ...)?

368. Пересечение трёх прямых круговых цилиндров, оси которых взаимно перпендикулярны (но не обязательно пересекаются), а радиусы равны 1, содержится в некотором шаре, радиус которого равен квадратному корню из числа 1,5. Докажите это.

369*. Высоты остроугольного треугольника ABC пересекаются в точке H. Окружность с центром H лежит внутри треугольника. Постройте треугольник A'B'C', описанный около неё и вписанный в треугольник ABC.

370*. Рассмотрим тройку неотрицательных чисел: a, b, c. Рассмотрим абсолютные величины разностей этих чисел: ½a – b½, ½b – c½,½c – a½. Затем из этой тройки по тому же правилу образуем следующую, затем следующую и так далее. Обязательно ли среди полученных таким образом чисел встретится 0, если исходные числа а) целые; б) действительные?

371. В каждой клетке шахматной доски написано целое число от 1 до 64, причём в разных клетках — разные числа. За один вопрос можно, указав любое множество полей, узнать множество чисел, стоящих на этих полях. За какое наименьшее число вопросов можно узнать числа во всех клетках?

372. Дан треугольник ABC. Докажите, что величина угла ACB не меньше 120° в том и только том случае, когда для любой точки P сумма длин отрезков AP, BP и CP не меньше суммы длин отрезков AC и BC.

373. а) Все натуральные числа (записанные в десятичной системе) разбиты на два класса. Докажите, что любую бесконечную десятичную дробь можно разрезать на такие конечные куски, чтобы все они, кроме, быть может, первого куска, принадлежали одному классу.

б) Та же задача, но натуральные числа разбиты не на два, а на несколько классов.

374. Числа a, b, c — положительные, a > c и b > c. Докажите, что сумма квадратных корней из чисел c(a – c) и c(b – c) не превосходит квадратного корня из числа ab.

375. Внутри выпуклого многогранника объёмом 1 отмечены 3(2ⁿ – 1) точки. Докажите, что из него можно вырезать выпуклый многогранник объёмом 1 ⁄ 2ⁿ, не содержащий внутри себя ни одной отмеченной точки.

376. а) В ряд расположено 30 клеток. На самой правой клетке стоит белая фишка, на самой левой — чёрная. Каждый из двух играющих по очереди передвигает свою фишку на одно поле — вперёд или назад. (Пропускать ход нельзя.) Проигравший — тот, кто не может сделать ход. Кто выигрывает: начинающий или его партнёр?

б) Решите задачу, заменив в условии 30 на n.

377. Дан треугольник АВС. Найдите на стороне АС такую точку D, чтобы периметр треугольника АВD равнялся длине стороны ВС.

378*. Существует бесконечно много натуральных чисел, не представимых в виде а) x³ + y³ + z³, где x, y, z — целые числа; б) x₁ⁿ + x₂ⁿ + ... + x_nⁿ, где x₁, x₂, ..., x_n — целые числа. Докажите это.

в) Любое рациональное число представимо в виде суммы кубов трёх рациональных чисел. Докажите это.

379*. На каждом из нескольких кусков бумаги произвольной формы поставлена клякса (произвольной формы). Назовём промокашку подходящей для данного куска, если её можно разместить внутри этого куска так, что она закроет кляксу. Пусть набор промокашек, имеющих форму кругов разных радиусов, обладает таким свойством: для любых двух данных кусков найдётся промокашка, подходящая для каждого из них. Докажите, что тогда в этом наборе найдётся одна промокашка, подходящая для всех кусков.

380*. а) На плоскости дана выпуклая фигура и внутри неё — точка O. К каждой прямой l, проходящей через точку О, проведём перпендикуляр в точке О и на нём по обе стороны от точки О отложим два равных отрезка, длины которых равны длине отрезка, получающегося при пересечении данной фигуры с прямой l. Объединение всех этих отрезков — новая фигура с центром симметрии О. Будет ли полученная фигура выпуклой?

б) В пространстве дано выпуклое центрально-симметричное тело с центром O. К каждой плоскости α, проходящей через точку O, проведём перпендикуляр в точке O и на нём по обе стороны от точки O отложим два отрезка, длины которых равны площади сечения данного тела плоскостью α. Объединение всех этих отрезков — новое тело с тем же центром симметрии О. Докажите, что полученное тело тоже выпуклое.

381. 6 активистов класса образовали 30 различных комиссий. Каждые две комиссии отличаются составом, но обязательно «пересекаются», то есть имеют общего члена. Докажите, что можно образовать ещё одну комиссию, пересекающуюся с каждой из этих 30 комиссий.

382. Если ни одно из значений многочлена с целыми коэффициентами в нескольких последовательных целых точках не делится на количество этих целых точек, то многочлен не имеет ни одного рационального корня. Докажите это.

383. Если произведение двух натуральных чисел чётно, то сумму их квадратов можно представить в виде разности квадратов натуральных чисел, а если нечётно, то нельзя. Докажите это.

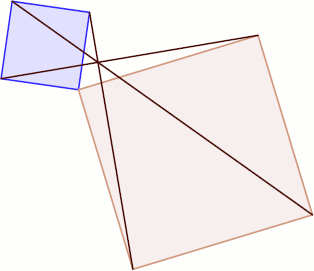384. Если квадраты OABC и OA'B'C' одинаково ориентированы, то прямые AA', BB' и CC' проходят через одну точку. Докажите это. (Два многоугольника называем одинаково ориентированными, если обход одного из них происходит в ту же сторону, что аналогичный обход другого, то есть оба по часовой стрелке или оба — против.)

385*. На клетчатой бумаге нарисован выпуклый многоугольник с вершинами в узлах (то есть углах клеток). Выберем какую-нибудь вершину O многоугольника F и обозначим через nF многоугольник, полученный из F растяжением в n раз относительно точки O (число n — натуральное). Обозначим через N(F) количество узлов, которые лежат внутри или на границе F, а через M(F) — количество узлов, лежащих на границе многоугольника F. Через S(F) обозначим площадь многоугольника F (площадь одной клетки равна 1). Докажите, что

а) N(nF) является многочленом от n;

б) 2S(F) = N(2F) – 2N(F) + 1;

в) S(F) = N(F) – ^M(F) ⁄ ₂ +1;

г) для любых двух выпуклых многоугольников F и G с вершинами в узлах N(nF + mG) является многочленом от m и n (имеется в виду сумма Минковского, о которой рассказано, например, в статье Н.Б. Васильева «Сложение фигур» в «Кванте» номер 4 за 1976 год). В трёхмерном пространстве рассмотрим выпуклый многогранник F, координаты всех вершин которого целые. Обозначим через nF многогранник, полученный из F гомотетией с коэффициентом n и центром в начале координат; через N(F) — количество точек с целыми координатами, расположенных внутри или на границе многогранника F; M(F) — количество точек с целыми координатами, расположенных на границе многогранника; V(F) — объём многогранника.

д) Не существует формулы, которая выражает V(F) через N(F) и M(F). Докажите это.

е) Придумайте формулу, которая (для некоторого k) выражает V(F) через N(F), N(2F), ..., N(kF).

ж) Придумайте формулу, выражающую V(F) через N(F), N(2F), M(F) и M(2F).

з) Докажите формулы, полученные при решении пунктов е) и ж).

и) N(nF) является многочленом от n. Докажите это.

386. Квадратная комната разгорожена перегородками на несколько меньших квадратных комнат. Длина стороны каждой комнаты — целое число. Докажите, что сумма длин всех перегородок делится на 4.

387*. Существует ли такое натуральное число, что если приписать его само к себе, то получится точный квадрат?

388. а) На плоскости отмечено конечное число точек. Докажите, что среди них найдётся точка, у которой не более трёх ближайших (то есть находящихся на наименьшем от нее расстоянии; таких точек, вообще говоря, может быть несколько).

б) Существует ли на плоскости конечное множество точек, у каждой из которых в этом множестве ровно три ближайших?

389. Можно ли бесконечный лист клетчатой бумаги разбить на «доминошки» (каждая доминошка покрывает две клетки) так, чтобы каждая прямая, идущая по линии сетки, разрезала пополам лишь конечное число доминошек?

390*. Существует бесконечно много таких натуральных чисел n, что сумма цифр десятичной записи числа 2ⁿ больше суммы цифр десятичной записи числа 2^{n + 1}. Докажите это.

391. а) В последовательности x₀, x₁, x₂, ... числа x₀ и x₁ — натуральные и меньшие 1000, а каждое следующее вычисляем по формуле x_n+2 = |x_n+1 – x_n|. Докажите, что хотя бы один из первых 1 500 членов последовательности равен 0.

б) В последовательности y₀, y₁, y₂, ... числа y₀ и y₁ — натуральные и меньшие 100 00, а каждое следующее равно наименьшей из абсолютных величин разностей некоторых двух предыдущих чисел. Докажите равенство x₂₀ = 0.

392. По трём прямолинейным дорогам с постоянными скоростями идут три пешехода. В начальный момент они не находились на одной прямой. Докажите, что они могут оказаться на одной прямой не более двух раз.

393. Найдите сумму f (0) + f (1 ⁄ n) + f (2 ⁄ n) + ... + f (n – 1 ⁄ n) + f (1), где f (x) = 4^x⁄ (4^x + 2).

394. а) На плоскости даны четыре вектора, сумма которых равна нулю. Рассмотрим суммы первого из них с каждым из остальных трёх, вычислим длины полученных сумм. Докажите, что сумма длин полученных трёх векторов не меньше суммы длин исходных четырёх векторов.

Докажите аналогичное неравенство для б) четырёх чисел, сумма которых равна нулю; в) четырёх векторов трёхмерного пространства, сумма которых равна нулю.

395*. В вершинах правильного n-угольника с центром в точке O расставлены числа 1 и –1. За один шаг разрешено изменить знак у всех чисел, стоящих в вершинах правильного k-угольника с центром O (при этом разрешены и «двуугольники» — отрезки с серединой в точке O). Докажите существование такого первоначального расположения единиц и минус единиц, что из него ни за какое число шагов нельзя невозможно получить набор из одних только 1, при а) n = 15; б) n = 30; в) n — любое натуральное число, n > 2.

г) Выясните для произвольного n, сколько существует типов расстановок, то есть каково наибольшее количество элементов в множестве расстановок чисел 1 и –1, ни одну из которых нельзя получить ни из какой другой расстановки этого множества при помощи интересующих нас операций. Например, докажите, что для n = 2100 существует 2⁴⁸⁰ таких расстановок.

396. Треугольник, все стороны которого больше 1, назовём большим. Докажите, что а) из треугольника Δ, длины всех сторон которого равны 5, можно вырезать 1000 больших треугольников; б) треугольник Δ можно разрезать на 1000 больших треугольников; в*) треугольник Δ можно триангулировать на 1000 больших треугольников, то есть разбить его так, чтобы любые два треугольника либо не имели общих точек, либо имели только общую вершину, либо имели общую сторону; г*) решите пункты б)и в) для равностороннего треугольника со стороной длины 3.

397. На плоскости даны три окружности одинакового радиуса. Докажите, что если они а) пересекаются в одной точке, как показано на левом рисунке, то сумма величин отмеченных дуг AK, CK и EK равна 180°; б) расположены так, как показано на правом рисунке, то сумма величин отмеченных дуг AB, CD и EF равна 180°.

398. На окружности расположены n чисел, сумма которых равна нулю. Одно из этих чисел равно 1.

а) Существуют соседние числа, различающиеся не менее чем на ⁴⁄_n. Докажите это.

б) Если n > 2, то хотя бы одно из чисел отличается от среднего арифметического своих соседей не менее чем на ⁸⁄_n². Докажите это.

в) Оценку, предложенную в предыдущем пункте, можно улучшить — заменить в ней число 8 каким-нибудь большим числом так, чтобы утверждение этой задачи по-прежнему выполнялось для всех натуральных чисел.

г*) Докажите, что для n = 30 на окружности есть число, отличающееся от среднего арифметического двух своих соседей не менее чем на ²⁄₁₁₃. Приведите пример набора 30 чисел на окружности, в котором ни одно число не отличается от среднего арифметического двух своих соседей более чем на ²⁄₁₁₃.

д*) Найдите точную оценку разности между числом и средним арифметическим его соседей для любого n > 2.

399*. На отрезке длиной 7 можно расставить 5 точек так, чтобы для любого m = 1, 2, 3, ..., 7 нашлись две отмеченные точки на расстоянии m. Обозначим через k наименьшее количество точек, которые нужно поставить на отрезке длиной n так, чтобы для любого натурального m £ n, нашлись две отмеченные точки на расстоянии m.

а) Найдите k для n = 1, 2, 3, ..., 13.

б) Докажите неравенства 8n + 1 £ (2k – 1)² и (k + 1)² £ 4n + 5.

400*. Последовательность натуральных чисел a₁, a₂, ..., a_k назовём универсальной для данного n, если из неё можно получить вычёркиванием части членов любую перестановку чисел от 1 до n, то есть любую последовательность из n чисел, в которую каждое из чисел от 1 до n входит по одному разу. Приведите пример универсальной последовательности из а) n²; б) n² – n + 1 членов.

в) Любая универсальная последовательность состоит не менее чем из n(n + 1) ⁄ 2 членов. Докажите это.

г) При n = 4 кратчайшая универсальная последовательность состоит из 12 членов. Докажите это.

д) Для каждого натурального n постарайтесь указать как можно более короткую универсальную последовательность.

401. Внутри остроугольного треугольника ABC расположена такая точка P, что величины углов APB, BPC и CPA на 60° больше соответственно величин углов ACB, BAC и CBA. Докажите, что точки пересечения продолжений отрезков АР, ВР, СР (за точку Р) с окружностью, описанной вокруг треугольника АВС, лежат в вершинах равностороннего треугольника.

402. Строго возрастающая последовательность a₁, a₂, a₃, ... целых неотрицательных чисел, для каждых натуральных m и n удовлетворяющая равенству a_mn = a_m + a_n, не существует. Докажите это.

403. Если в выпуклом многограннике из каждой вершины выходит чётное число рёбер, то любое сечение плоскостью, не проходящей ни через одну из вершин, является многоугольником с чётным числом сторон. Докажите это.

404. На полке стоят первые n томов энциклопедии, где n > 3. Позволено взять любые три рядом стоящих тома и поставить их между любыми двумя томами или же в начало или в конец ряда, не меняя при этом порядка этих трёх томов. Всегда ли можно, применив несколько раз указанную операцию, расставить их в порядке возрастания номеров томов (независимо от первоначальной расстановки томов)?

405. На шахматной доске размером 99×99 отмечена фигура Ф. В каждой клетке фигуры Ф сидит жук. В какой-то момент жуки взлетели и сели снова в клетки той же фигуры Ф; при этом в одну клетку могли сесть несколько жуков. После перелёта любые два жука, занимавшие соседние клетки, оказались снова в соседних клетках или попали на одну клетку. (Соседними называем клетки, имеющие общую сторону или общую вершину.)

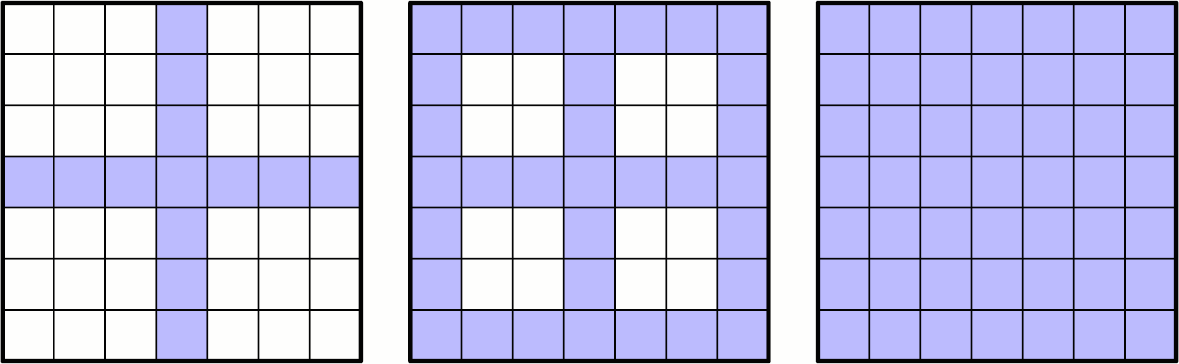
а) Пусть Ф — «центральный крест». Докажите, что в таком случае какой-то жук вернулся на место или перелетел на соседнюю клетку.

б) Верно ли это утверждение, если Ф — «оконная рама»?

в) А если Ф — вся доска?

406. Квадрат ABCD вписан в окружность радиуса R. Докажите для любой точки M этой окружности равенство AM⁴ + BM⁴ + CM⁴ + DM⁴ = 24R⁴.

407. m и n — натуральные числа, причём n > m. Докажите, что n представимо в виде суммы двух натуральных чисел, одно из которых — делитель числа m, а другое взаимно просто с ним, то есть не имеет с m ни одного общего делителя, кроме единицы.

408. Из 30 равных прямоугольников составлен прямоугольник, подобный исходным. Каким может быть отношение длин сторон этого прямоугольника?

409*. В строку подряд написано 1000 чисел. Под каждым числом a первой строки напишем число, указывающее, сколько раз число a встречается в первой строке. Из полученной таким образом второй строки аналогично получаем третью: под каждым числом второй строки пишем, сколько раз оно встречается во второй строке. Затем из третьей строки так же получаем четвёртую, из четвёртой — пятую, и так далее.

а) Докажите, что некоторая строчка совпадает со следующей.

б) Докажите, что 11-я строка совпадает с 12-й.

в) Приведите пример такой первоначальной строчки, для которой 10-я строка не совпадает с 11-й.

410*. На сфере с радиусом 1 проведена окружность большого круга, которую мы будем называть экватором. Будем использовать и другие географические термины: полюс, меридиан, параллель.

а) Зададим на этой сфере функцию f, значение которой в каждой данной точке M равно квадрату расстояния от M до плоскости экватора. Проверьте для любых трёх концов X, Y, Z трёх взаимно перпендикулярных радиусов сферы равенство f (X) + f (Y) + f (Z) = 1.     (*)

В следующих пунктах f — произвольная неотрицательная функция на сфере, которая равна 0 во всех точках экватора и обладает свойством (*).

б) Пусть M и N — точки одного меридиана, расположенные между северным полюсом и экватором. Докажите, что если точка M расположена дальше от плоскости экватора, чем N, то f (M) ³ f (N).

в) Докажите, что функция f совпадает с функцией, описанной в пункте а).

411. Три отрезка с концами на сторонах треугольника, параллельные его сторонам, проходят через одну точку и имеют одинаковую длину х. Выразите х через длины a, b и c сторон треугольника.

412. В городе на каждую площадь выходит не менее трёх улиц. На всех улицах введено одностороннее движение так, что с любой площади можно проехать на любую другую. Докажите, что можно запретить движение по одной из улиц (на участке между двумя площадями) так, что по-прежнему с любой площади можно будет проехать на другую.

413. Для каких положительных чисел a верно следующее утверждение: для любой функции f, определённой на отрезке [0; 1], непрерывной в каждой точке этого отрезка и такой, что f (0) = f (1) = 0, уравнение f (x + a) = f (x) имеет решение?

а) Рассмотрите сначала случай a = ¹⁄₂.

б) Для a = ¹⁄_n, где n — натуральное число, докажите сформулированное утверждение.

в) Для остальных положительных a утверждение ложно. Докажите это.

При решении задачи может пригодиться такое свойство непрерывных функций: если функция g определена на отрезке [a; b], непрерывна в каждой точке этого отрезка и на концах его принимает значения разных знаков, то между a и b найдётся такая точка c, что g (c) = 0.

414*. а) Из пяти треугольников, отсекаемых от данного выпуклого пятиугольника его диагоналями, площади четырёх равны S, а площадь пятого — 3S ⁄ 2. Найдите площадь x этого пятиугольника.

б) Если S₁, S₂, S₃, S₄ и S₅ — площади пяти таких треугольников, то x² – (S₁ + S₂ + S₃ + S₄ + S₅)x + S₁S₂ + S₂S₃ + S₃S₄ + S₄S₅ + S₅S₁ = 0.

415. Какое наибольшее число королей можно расставить на торической шахматной доске n×n, чтобы они не били один другого? Торическую шахматную доску получаем из обычной доски, склеивая её верхнюю горизонталь с нижней, а левую вертикаль с правой. На торической доске с каждого поля король может пойти на любое из восьми соседних полей.

416. В пространстве даны n точек, никакие четыре из которых не лежат на одной прямой. Какое наибольшее число отрезков с концами в этих точках можно провести так, чтобы не получилось ни одного треугольника с вершинами в этих точках?

417. На поверхности куба с ребром 1 расположена замкнутая ломаная линия. На каждой грани куба находится по крайней мере одна её точка. Докажите, что длина ломаной не меньше 3 квадратных корней из двух.

418. Для любого натурального n докажите, что сумма обратных величин первых n натуральных чисел не меньше произведения числа n и разности корня n-й степени из n + 1 и числа 1 и не больше суммы числа 1 и произведения числа n на разность числа 1 и числа, обратного корню n-й степени из n.

419. В круге радиусом 16 расположены 650 точек. Докажите существование кольца с внутренним радиусом 2 и внешним радиусом 3, в котором лежат не менее 10 из данных точек.

420. а) Из дроби ^a⁄_b, где a ≠ 0, разрешено получить любую из трёх дробей ^{(a – b)}⁄_b, ^{(a + b)}⁄_b и ^b⁄_a. (В том числе при a £ 0; таким образом, мы рассматриваем дробь лишь как пару чисел, допуская в знаменатель ноль и отрицательные числа.) Можно ли такими преобразованиями из дроби ¹⁄₂ получить дробь ⁶⁷⁄₉₁?

б*) Из пары дробей (^a⁄_b; ^c⁄_d) разрешено получить любую из пар (^{(a + b)}⁄_b; ^{(c + d)}⁄_d), (^{(a – b)}⁄_b; ^{(c – d)}⁄_d), (^b⁄_a; ^d⁄_c) (в том числе при a = 0 или с = 0). Можно ли из пары дробей (¹⁄₂; ⁵⁄₇) получить следующие пары: (¹⁄₃; ²⁄₉), (¹⁄₄; ³⁄₈), (⁴⁄₅; ⁷⁄₈), (⁵⁄₁₉; ¹³⁄₅₀) и (³⁹⁄₅₀; ⁶⁰⁄₇₇)?

в*) Постарайтесь выяснить, какие вообще «дроби» (соответственно, пары «дробей» с возможно равными нулю знаменателями) можно получить из данных в пунктах а) и б).