421. При каких натуральных m и n, где m £ n, можно закрасить некоторые клетки бесконечного листа клетчатой бумаги таким образом, чтобы любой прямоугольник размером m×n содержал ровно одну закрашенную клетку? (Начните с частных случаев m = 2 и n = 3, 4 или 5.)

422. Разбейте произвольный треугольник на семь равнобедренных треугольников, из которых три равны между собой.

423*. Для любых вещественных чисел x, y и z докажите, что произведение (x² + y² – z²)(x² + z² – y²)(y² + z² – x²) не превосходит квадрата произведения (x + y – z)(x + z – y)(y + z – x). Докажите это.

424. Через каждую вершину тетраэдра проведена плоскость, содержащая центр окружности, описанной около противоположной грани, и перпендикулярная противоположной грани. Докажите, что эти четыре плоскости пересекаются в одной точке.

425*. Существует ли такое натуральное n, что каждое рациональное число между нулём и единицей представимо в виде суммы n чисел, обратных натуральным?

1 2 3 4     ...   n – 1 n 2 3 4     ...   n – 1 n 1 3 4     ...   n – 1 n 1 2 4     ...   n – 1 n 1 2 3     ...   n – 1 n 1 2 3 4   ...   n – 1 n 1 2 3 4   ...   n – 1 n 1 2 3 4       n – 1 n 1 2 3 4     ... n – 1 n 1 2 3 4     ... n – 2 n 1 2 3 4     ... n – 2 n – 1

426. Таблица размером n×n заполнена числами от 1 до n, как показано на рисунке. При каких n в ней можно выбрать n клеток так, чтобы никакие две клетки не принадлежали одной строке или одному столбцу и чтобы все числа в выбранных клетках были разные?

427. Докажите следующие утверждения.

а) Существует такое нечётное число n, что ни для какого чётного k ни одно из чисел k^k + 1, k^kk + 1, k^kkk + 1, k^kkkk + 1, ... не делится на n.

б) Для любого натурального n существует такое натуральное k, что все члены последовательности k^k + 1, k^kk + 1, k^kkk + 1, k^kkkk + 1, ... делятся на n.

428. В олимпиаде участвуют (m – 1) · n + 1 человек. Докажите, что среди них найдутся m участников, попарно незнакомых между собой, либо найдётся участник, знакомый не менее чем с n участниками олимпиады. Останется ли верным утверждение задачи, если количество участников олимпиады уменьшится на единицу? (Отношение знакомства считаем симметричным: если Дутин знаком с Жутиным, то и Жутин знаком с Дутиным.)

429. а) Сколько решений имеет уравнение [x] – 1977{x} = 1978?

б) Если p не равно 0, то для любого q уравнение [x] + p{x} = q имеет [|p|] или [|p|] + 1 решений. Докажите это.

430*. а) Любую выпуклую плоскую фигуру площади S можно поместить в прямоугольник площади 2S. Докажите это.

б) Любое выпуклое тело объёма V можно поместить в прямоугольный параллелепипeд объёма 6V. Докажите это.

431. В лесу растут деревья цилиндрической формы. Связисту нужно протянуть по лесу провод из точки А в точку В, расстояние между которыми равно l. Докажите, что для этой цели достаточно иметь провод длиной 1,6 l.

432*. Существует ли натуральное число, сумма цифр десятичной записи квадрата которого равна а) 1977; б) 1978?

в) Какие натуральные числа являются суммами цифр десятичной записи квадрата целого числа?

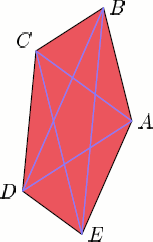433. Сторона ВС выпуклого пятиугольника ABCDE параллельна диагонали AD, сторона CD — диагонали ВЕ, сторона DE — диагонали AC, а сторона АЕ — диагонали BD. Докажите, что сторона АВ параллельна диагонали СЕ.

434*. Для каждого натурального n представим сумму дробей вида 2^k ⁄ k, где k = 1, 2, ..., n, в виде несократимой дроби p ⁄ q. Докажите следующие утверждения.

а) Все числа p₁, p₂, p₃, ... чётные.

б) Если n > 3, то p_n делится на 8.

в) Для любого натурального k существует такое n, что все числа p_n, p_n+1, p_n+2, ... делятся на 2^k.

435*. В таблице размером m×n записаны действительные числа, в каждой клетке по числу. Пусть k £ m и l £ n. В каждом столбце подчеркнём k наибольших чисел, а в каждой строке — l наибольших чисел. Докажите, что по крайней мере kl чисел подчёркнуты дважды. Разберите случаи а) k = l = 2; б) k = l = 3; в) k и l — любые.

436. Даны 20 чисел a₁, a₂, a₃, ..., a₁₀, b₁, b₂, ..., b₁₀. Докажите, что набор из 100 чисел (не обязательно различных), получаемых сложением одного из чисел a_k с одним из чисел b_m, можно так разбить на 10 подмножеств, по 10 чисел в каждом, чтобы сумма элементов подмножества была одна и та же для всех подмножеств.

437. Нечётное число, являющееся произведением n различных простых чисел, представимо в виде разности квадратов двух натуральных чисел ровно 2^n–1 способами. Докажите это. (Например, число 5 · 13 можно представить двумя способами: 65 = 9² – 4² = 33² – 32².)

438. В данный сегмент вписываем всевозможные пары касающихся окружностей. Для каждой пары окружностей через точку касания проводим касающуюся их прямую. Докажите, что все эти прямые проходят через одну точку.

439*. а) Уравнение ax^k + bx^l + cx^m = 1, где a, b и c — действительные, а k, l и m — натуральные числа, имеет не более трёх положительных корней. Докажите это.

б) Уравнение, в левой части которого находится сумма n слагаемых вида ax^k, где k — натуральное число, а a — действительное число, имеет не более n положительных корней. Докажите это.

в) Уравнение ax^k(x + 1)^p + bx^l(x + 1)^q + cx^m(x + 1)^r = 1, где a, b и c — действительные, а k, l, m, p, q и r — натуральные числа, имеет не более 14 положительных корней. Докажите это.

440. Куб 100×100×100 составлен из миллиона единичных кубиков. Назовём шампуром прямую, проходящую через центры кубиков и параллельную рёбрам куба.

а) При каком наименьшем k можно провести k непересекающихся шампуров так, чтобы к ним нельзя было добавить ещё один не пересекающий их шампур?

б) При каком наибольшем k можно провести 3k непересекающихся шампуров так, чтобы среди них было k шампуров каждого направления?

441. Внутри выпуклого 2n-угольника взята произвольная точка Р. Через каждую вершину и точку Р проведена прямая. Докажите, что найдётся сторона многоугольника, с которой ни одна из проведённых прямых не имеет общих точек (кроме, быть может, концов стороны).

442. Пусть p — простое число, p > 2. Для каждого натурального числа k < p вычислим остаток от деления числа k^p на p². Докажите, что сумма вычисленных остатков равна половине разности p³ – p.

443. Рассмотрим таблицу размером n×n, все клетки которой заполнены нулями. Разрешено произвольно выбрать n чисел, стоящих в разных строках и разных столбцах, и увеличить каждое из них на 1.

а) Можно ли за несколько шагов получить таблицы, изображённые на рисунках?

1 2 3 4     ...   n – 1 n 2 3 4     ...   n – 1 n 1 3 4     ...   n – 1 n 1 2 4     ...   n – 1 n 1 2 3     ...   n – 1 n 1 2 3 4   ...   n – 1 n 1 2 3 4   ...   n – 1 n 1 2 3 4       n – 1 n 1 2 3 4     ... n – 1 n 1 2 3 4     ... n – 2 n 1 2 3 4     ... n – 2 n – 1

1 2 3 4     ...   n – 1 n 2 3 4     ...   n – 1 n n + 1 3 4     ...   n – 1 n n + 1 n + 2 4     ...   n – 1 n n + 1 n + 2 n + 3     ...   n – 1 n n + 1 n + 2 n + 3 n + 4   ...   n – 1 n n + 1 n + 2 n + 3 n + 4   ...   n – 1 n n + 1 n + 2 n + 3 n + 4       n – 1 n n + 1 n + 2 n + 3 n + 4     ... n – 1 n n + 1 n + 2 n + 3 n + 4     ... 2n – 2 n n + 1 n + 2 n + 3 n + 4     ... 2n – 2 2n – 1

б) Можно ли получить таблицу, ни одно число которой не равно никакому другому?

в*) Какие вообще таблицы можно получить через t шагов?

444. На рисунке четыре прямые разбивают плоскость на 11 областей: четырёхугольник, два треугольника, три угла, четыре «бесконечных треугольника» (области, ограниченные каждая отрезком и двумя лучами) и «бесконечный четырёхугольник» (область, ограниченная двумя отрезками и двумя лучами).

а) Верно ли сказанное для любых четырёх прямых на плоскости, среди которых нет параллельных и нет троек прямых, проходящих через одну точку?

б) Три больших круга, не проходящих через одну точку, разбивают круг на 8 треугольников. На какие области разбивают сферу четыре больших круга, никакие три из которых не проходят через одну точку? (Большим кругом на сфере называют окружность, являющуюся пересечением сферы с плоскостью, проходящей через её центр.)

в) На какие области могут разбить сферу 5 больших кругов, никакие три из которых не проходят через одну точку?

445. Центры одинаковых непересекающихся окружностей находятся в центрах правильных шестиугольниках, покрывающих плоскость так, как показано на рисунке. Пусть M — многоугольник с вершинами в центрах окружностей. Окрасим те окружности или их дуги, которые лежат внутри M, как показано на рисунке. Докажите, что сумма величин окрашенных дуг равна 180°·n, где n — натуральное число, и дайте этому геометрическую интерпретацию.

446. Окружность радиуса 1 катится снаружи по окружности, квадрат длины которой равен 2. В начальный момент времени точка касания окружностей отмечена липкой красной краской. При качении любая покрашенная точка красит любую точку, с которой соприкасается. Сколько разных точек неподвижной окружности будут запачканы к тому моменту, когда подвижная окружность сделает 100 оборотов вокруг неподвижной?

447*. В остроугольном треугольнике ABC отрезки BO и CO, где O — центр описанной окружности, продолжены до пересечения в точках D и E со сторонами AC и BC. Найдите величины углов треугольника ABC и докажите равенства AE = ED, CE = CB и CD = CO, если величины углов BDE и CED равны 50° и 30° соответственно.

448*. Центр любого эллипса, вписанного в данный четырёхугольник, лежит на прямой, проходящей через середины диагоналей этого четырёхугольника. Докажите это.

449. а) По одной прямой двигаются n одинаковых шариков. Какое максимальное число соударений между ними может произойти?

б*) Тот же вопрос для трёх шариков массами m₁, m₂ и m₃.

в*) Если по одной прямой двигаются n различных шариков, то общее число столкновений между ними конечно. Докажите это.

В этих задачах шарики — это материальные точки, сталкивающиеся друг с другом абсолютно упруго, то есть с сохранением суммарных импульса и энергии, причём предполагаем, что все происходящие столкновения — только парные: три или более шарика в одной точке одновременно не оказываются.

450. Система прямоугольников из n этажей построена следующим образом. Начиная с нижнего прямоугольника, образующего первый этаж, верхнюю сторону каждого прямоугольника делим в отношении 1 : 2 : 3; на трёх полученных отрезках как на основаниях строим прямоугольники той же высоты, что и первоначальный, и так — до самого верхнего этажа. Из полученного множества прямоугольников выбрано некоторое подмножество, состоящее из попарно неравных прямоугольников (одно такое подмножество на рисунке выделено). Докажите существование вертикальной прямой, пересекающей не более двух из выбранных прямоугольников.

451. На плоскости отмечено несколько точек, не лежащих на одной прямой, и около каждой написано число. Для любой прямой, проходящей через две или более отмеченные точки, сумма всех чисел, написанных около этих точек, равна 0. Докажите, что все числа равны 0.

452. В окружность вписаны треугольники T₁ и T₂, причём вершины треугольника T₂ являются серединами дуг, на которые окружность разбивается вершинами треугольника T₁. Докажите, что диагонали шестиугольника, являющегося пересечением треугольников T₁ и T₂, соединяющие его противоположные вершины, параллельны сторонам треугольника T₁ и пересекаются в одной точке.

453*. Множество состоит из n положительных чисел. Для каждого его непустого подмножества выпишем сумму его элементов. Докажите, что все 2ⁿ – 1 выписанных сумм можно так разбить на n множеств, что в каждом из них отношение наибольшего числа к наименьшему не превзойдёт числа 2.

454. За круглым столом сидят 7 гномов. Перед каждым стоит кружка. В некоторые из этих кружек налито молоко. Один из гномов разливает всё своё молоко в кружки остальных поровну. Затем его сосед справа делает то же самое. Затем то же самое делает следующий сосед справа и так далее. После того как седьмой гном разлил всем остальным своё молоко, в каждой кружке оказалось столько же молока, сколько было в ней вначале. Во всех кружках вместе молока 3 литра. Сколько молока было первоначально в каждой кружке?

455. Мы будем рассматривать многочлены от одной переменной со старшим коэффициентом 1. Будем говорить, что два таких многочлена P и Q коммутируют, если многочлены P(Q(х)) и Q(Р(х)) тождественно равны (то есть после раскрытия скобок и приведения к стандартному виду все коэффициенты этих многочленов совпадают).

а) Для любого числа α найдите все многочлены степени не выше третьей, коммутирующие с многочленом x² – α.

б) Пусть P — многочлен степени 2, k — натуральное число. Докажите, что существует не более одного многочлена степени k, коммутирующего с P.

в) Найдите все многочлены степени 4 или 8, коммутирующие с данным многочленом P степени 2.

г) Если два многочлена коммутируют с одним и тем же многочленом второй степени, то они коммутируют между собой. Докажите это.

д) Существует бесконечная последовательность многочленов P₁, P₂, P₃, ..., каждые два члена которой коммутируют, а P₂(x) = x² — 2. Докажите это.

456. В каждой вершине выпуклого многогранника сходятся 3 ребра, а каждая его грань является многоугольником, вокруг которого можно описать окружность. Докажите, что вокруг этого многогранника можно описать сферу.

457. На плоскости дана несамопересекающаяся замкнутая ломаная, никакие три вершины которой не лежат на одной прямой. Назовём пару несоседних звеньев особенной, если продолжение одного из них пересекает другое. Докажите, что число особенных пар чётно.

458. Напишем многочлен десятой степени, старший коэффициент которого равен 1, как и его свободный член. Остальные 9 коэффициентов этого многочлена заменим на звёздочки. Пусть теперь двое играют в такую игру. Сначала первый заменяет одну из звёздочек некоторым числом, затем второй заменяет числом любую из оставшихся звёздочек, затем снова первый заменяет одну из звёздочек числом и так далее (всего 9 ходов). Если у полученного многочлена не будет действительных корней, то выигрывает первый игрок, а если будет хотя бы один корень — выигрывает второй. Может ли второй игрок выиграть при любой игре первого?

459*. В некоторой стране из каждого города в другой можно проехать, минуя остальные города. Известна стоимость каждого такого проезда. Составлены два маршрута поездок по городам страны. В каждый из этих маршрутов каждый город входит ровно по одному разу. При составлении первого маршрута руководствовались следующим принципом: начальный пункт маршрута выбрали произвольно, а на каждом следующем шаге среди городов, через которые маршрут ещё не прошёл, выбирали тот, поездка в который из предыдущего города имеет наименьшую стоимость (если таких городов несколько, то выбирали любой из них), и так до тех пор, пока не пройдены все города. При составлении второго маршрута начальный город тоже выбрали произвольно, а на каждом следующем шаге среди городов, через которые маршрут ещё не прошёл, выбирали тот, поездка в который из предыдущего города имеет наибольшую стоимость. Докажите, что общая стоимость проезда по первому маршруту не больше общей стоимости проезда по второму маршруту.

460. Пусть А — 2n-значное число (первая цифра не нуль). Будем называть число А особым, если как оно само, так и числа, образованные его первыми n цифрами и его последними n цифрами, являются квадратами целых чисел; при этом второе число может начинаться с цифры 0, но не должно быть равно нулю.

а) Найдите все двузначные и четырёхзначные особые числа.

Существует б) хотя бы одно 20-значное особое число; в) не более 10 особых 100-значных чисел; г) хотя бы одно 30-значное особое число. Докажите это.

461. На столе стоят чашечные весы и n гирь различных масс. Гири по очереди ставим на чашки весов (на каждом шаге со стола берём любую гирю и добавляем на ту или другую чашку весов).

а) Докажите, что гири можно ставить в таком порядке, чтобы сначала перевесила левая чашка, затем правая, потом снова левая, снова правая и так далее.

Этой последовательности результатов взвешиваний сопоставим слово из букв L и R: LRLRLRLR... Здесь буква L (left) означает, что перевесила левая чашка, а буква R (right) означает, что перевесила правая чашка.

б)* Для любого слова длиной n из букв L и R можно в таком порядке ставить гири на чашки весов, чтобы это слово соответствовало последовательности результатов взвешиваний.

462. Плоскость пересекает боковые ребра правильной четырёхугольной пирамиды в точках, отстоящих от вершины на расстояния a, b, с и d. Докажите равенство ¹⁄_a + ¹⁄_c = ¹⁄_b + ¹⁄_d.

463*. Если сумма натуральных чисел x₁, x₂, ..., x_m равна сумме натуральных чисел y₁, y₂, ..., y_n и эта сумма меньше mn, то можно вычеркнуть часть слагаемых так, чтобы равенство осталось верным. Докажите это.

464*. На плоскости даны 1000 квадратов со сторонами, параллельными осям координат. Пусть М — множество центров этих квадратов. Докажите, что можно отметить часть квадратов так, чтобы каждая точка множества М попала не менее чем в один и не более чем в четыре отмеченных квадрата.

465*. Имеется тысяча билетов с номерами 000, 001, ..., 999 и сто ящиков с номерами 00, 01, ..., 99. Билет разрешено опустить в ящик, если номер ящика можно получить из номера этого билета вычёркиванием одной из цифр. Докажите, что а) можно разложить все билеты в 50 ящиков; б) нельзя разложить все билеты менее, чем в 40 ящиков; в) нельзя разложить все билеты менее, чем в 50 ящиков.

Пусть вообще имеется 10^k билетов с k-значными номерами (от 00...0 до 99...9). Билет разрешено опустить в ящик, номер которого можно получить из номера этого билета вычёркиванием некоторых k – 2 цифр. г) Докажите, что при k = 4 все 10 000 четырёхзначных билетов можно разложить по 34 ящикам.

д) Найдите минимальное количество ящиков, в которое можно разложить k-значные билеты. Попробуйте решить эту задачу для k = 4, 5, 6, ...

466. Среди 1977 монет 50 фальшивых. Каждая фальшивая монета отличается от настоящей на один грамм (в ту или в другую сторону). Имеются чашечные весы со стрелкой, показывающей разность масс грузов на чашках. За одно взвешивание про одну выбранную монету нужно узнать, фальшивая она или настоящая. Научитесь это делать!

467. Точки D и E делят стороны AC и AB правильного треугольника ABC в отношениях AD : DC = BE : EA = 1 : 2. Прямые BD и CE пересекаются в точке О. Докажите, что угол АОС прямой.

468. Точки A, B, C и D таковы, что для любой точки M скалярное произведение векторов MA и MB равно скалярному произведению векторов MC и MD. Верно ли обратное утверждение?

469*. а) Если уравнение x⁴ + ax³ + bx + c = 0 имеет четыре различных вещественных корня, то ab < 0. Докажите это.

б) Если уравнение xⁿ + a_n–1x^n–1 + ... + a_k+1x^k+1 + a_k–1x^k–1 + ... + a₀ = 0 имеет n различных вещественных корней, то a_k+1a_k–1 < 0. Докажите это.

470. Докажите следующие утверждения.

а) Сумма выражений вида (–1)^k⁄ C_n^k, где 0 £ k £ n, равна числу (n + 1)((–1)ⁿ + 1) ⁄ (n + 2).

б) Сумма выражений вида 1 ⁄ C_n^k, где 0 £ k £ n, равна сумме чисел вида 2^k⁄ k, где 1 £ k £ n, умноженной на (n + 1) и делённой на 2ⁿ⁺¹.

471. Две пересекающиеся окружности вырезают из плоскости три ограниченные непересекающиеся области. Докажите, что не существует окружности, делящей пополам площадь каждой из этих трёх областей.

472. Внутри куба расположен выпуклый многогранник, проекция которого на каждую из граней совпадает с этой гранью. Докажите, что объём многогранника не меньше ¹⁄₃ объёма куба.

473*. Даны две группы по n гирь, в каждой из которых гири расположены в порядке возрастания масс. Докажите, что

а) 2n – 1 взвешиваниями можно расположить и все 2n гирь в порядке возрастания их масс;

б) меньшим 2n – 1 числом взвешиваний это сделать, вообще говоря, нельзя. (За одно взвешивание сравнивают массы двух гирь; массы всех гирь разные.)

474. Натуральное число называют совершенным, если оно равно половине суммы своих делителей. Докажите, что число несовершенно, если оно а) при делении на 4 даёт остаток 3; б) при делении на 6 даёт остаток 5.

Числа 6 = 1 + 2 + 3 и 28 = 1 + 2 + 4 + 7 + 14 совершенные. До сих пор неизвестно, существует ли нечётное совершенное число.

475*. а) Равносторонний треугольник нельзя нарисовать на клетчатой бумаге так, чтобы его вершины попали в узлы сетки (вершины клеток). Докажите это.

б*) На клетчатой бумаге со стороной клетки, равной 1, можно для любого положительного числа ε нарисовать равносторонний треугольник, вершины которого находятся на расстоянии меньше ε от трёх различных узлов бумаги. Докажите это.

в*) Для любого ли многоугольника M и любого ли положительного числа ε можно нарисовать на клетчатой бумаге многоугольник, подобный M, каждая вершина которого находится на расстоянии меньше ε от ближайшего и своего для каждой вершины узла?

476*. а) Если все вершины выпуклого многоугольника лежат в узлах клетчатой бумаги, а ни внутри, ни на его сторонах других узлов нет, то n < 555. Докажите это.

б) Пространство разбито тремя семействами параллельных плоскостей на одинаковые кубы. Вершины кубов назовём узлами. Докажите, что если все n вершин выпуклого многогранника лежат в узлах, а на его рёбрах, гранях и в его внутренности других узлов нет, то n < 9.

477*. Дан многочлен P с целыми коэффициентами такой, что для каждого натурального x верно неравенство x < P(x) . Определим последовательность формулами b₁ = 1 и b_k+1 = P(b_k) для каждого натурального k. Докажите, что если для любого натурального числа d хотя бы один из членов последовательности делится на d, то P(x) = x + 1.

478. В волейбольном турнире каждые две команды сыграли по одному матчу.

а) Если для любых двух команд найдётся третья, которая выиграла у этих двух, то число команд не меньше семи. Докажите это.

б) Постройте пример такого турнира семи команд.

в) Если для любых трёх команд найдётся такая, которая выиграла у этих трёх, то число команд не меньше 15. Докажите это.

479. Существуют ли а) 6; б) 1000 таких различных натуральных чисел, что для любых двух из них сумма этих двух чисел делится на их разность?

480*. Докажите следующие утверждения.

а) В последовательности, заданной начальным членом c₁ = 2 и рекуррентной формулой c_n+1 = [3c_n ⁄ 2], бесконечно много чётных чисел и бесконечно много нечётных чисел.

б) Последовательность остатков от деления на 2 чисел c₁, c₂, c₃, ... непериодическая.

в) Существует такое число γ, что для любого натурального числа n число c_n является наименьшим натуральным числом, большим произведения числа γ и n-й степени числа 3 ⁄ 2.