661. На берегу круглого озера четыре пристани K, L, P и Q. От пристани K отплывает катер, от L — лодка. Если катер поплывёт прямо в P, а лодка — прямо в Q, то они столкнутся в некоторой точке X озера. Докажите, что если катер поплывёт в Q, а лодка в P, то они достигнут этих пристаней одновременно.

662. В копилке собрано четыре рубля медными монетами (по 1, 3 и 5 копеек). Докажите, что этими монетами можно заплатить три рубля без сдачи.

663. Найдите все такие простые числа p, что число 2^p + p² тоже простое.

664*. Дан четырёхугольник ABCD. Обозначим точки пересечения высот треугольников ABC, BCD, CDA и DAB буквами N, K, L и M соответственно. Докажите равенство площадей четырёхугольников NKLM и ABCD.

665*. Световое табло состоит из нескольких ламп, каждая из которых может находиться в двух состояниях (гореть или не гореть). На пульте несколько кнопок, при нажатии каждой из которых одновременно меняется состояние некоторого набора ламп (для каждой кнопки — своего). Вначале лампы не горят.

а) Докажите, что число различных узоров, которые можно получить на табло,— степень двойки.

б) Сколько различных узоров можно получить на табло, состоящем из mn лампочек, расположенных в форме прямоугольника размером m×n, если кнопками можно переключить как любой горизонтальный, так и любой вертикальный ряд ламп? (Проверьте ваш ответ для небольших значений m и n.)

в) Придумайте другие примеры табло и наборов (переключаемых кнопками), в которых можно найти число узоров.

666. Наименьшее общее кратное любых n натуральных чисел a₁ < a₂ < ... < a_n не меньше na₁. Докажите это.

667. Постройте треугольник AВС, если заданы его наименьший угол A и отрезки с длинами d = AB – BC и e = AC – BC.

668*. Последовательность x₁, x₂, x₃,... определена условиями x₁ = 1, x₂ = 0, x₃ = 2, x_n+1 = x_n–2 + 2x_n–1. Докажите, что для любого натурального m существуют два соседних члена этой последовательности, каждый из которых кратен m.

669. Четырёхугольник ABCD вписан в окружность. Докажите, что

а) отрезок, соединяющий середины дуг AB и CD, перпендикулярен отрезку, соединяющему середины дуг BC и AD;

б) центры окружностей, вписанных в треугольники АВС, ВСD, СDA и DAB, являются вершинами прямоугольника.

670*. Дано несколько точек, некоторые пары которых соединены линиями (точки таких пар называем соседями). Число соседей у каждой точки нечётно. В начальный момент все точки раскрашены в два цвета — красный и синий. Затем каждую минуту происходит одновременное перекрашивание точек по следующему правилу: каждая точка, у которой большинство соседей имеет отличный от неё цвет, меняет свой цвет; в противном случае её цвет сохраняется. а) Докажите, что наступит момент, начиная с которого у некоторых точек цвет не будет меняться, а у некоторых будет меняться каждую минуту.

б) Останется ли это утверждение верным, если не предполагать, что у каждой точки число соседей нечётно?

671. Во вписанном четырёхугольнике одна диагональ делит вторую пополам. Докажите, что квадрат длины первой диагонали равен половине суммы квадратов длин всех сторон четырёхугольника.

672. Пусть a — такое натуральное число, что 2^a – 2 делится на a (например, a = 3). Рассмотрим последовательность, первый член которой равен x₁ = a, а каждый следующий член x_n+1, где n = 1, 2, 3,..., получаем, вычитая единицу из числа 2, возведённого в степень x_n. Докажите, что для любого натурального n число x_n является делителем числа 2^x_n – 2.

673. На плоскости в вершинах треугольника лежат три шайбы A, B и C. Хоккеист выбирает одну из них и бьёт по ней так, что она проходит между двумя другими и останавливается в какой-то точке.

а) Покажите, как после пяти ударов шайба сможет вернуться на своё место, а шайбы A и B поменяться местами.

б) Могут ли все три шайбы A, B и C вернуться на свои прежние места после 25 ударов?

674. На сторонах BC, CA и AB остроугольного треугольника взяты точки A', B' и С' соответственно. Центр описанной окружности треугольника ABC совпал с точкой пересечения высот треугольника A'B'C'. Докажите подобие треугольников ABC и A'B'C'.

675*. Системой разновесов назовём множество натуральных чисел, из которого нельзя извлечь два различных подмножества с одинаковой суммой (например, числа 24, 23, 22, 20, 17, 11 образуют систему разновесов, а числа 1, 2, 3, 4, 5, 8 не образуют: 2 + 3 + 4 = 1 + 8). Докажите, что из чисел, меньших 1000, можно выделить систему разновесов из а) 10; б) 11 чисел.

в) Докажите, что 14 чисел из них выбрать нельзя.

г) Докажите, что если числа образуют систему разновесов, то сумма их обратных величин не превосходит ⁵⁄₂.

д) Выберите из чисел, меньших 700, систему разновесов из 11 чисел.

676. Для любого натурального m сумма цифр десятичной записи числа 1981^m не меньше 19. Докажите это.

677. Внутри остроугольного треугольника АВС выбрана точка М, являющаяся точкой пересечения а) медиан; б) биссектрис; в) высот. Если радиусы окружностей, вписанных в треугольники АМВ, МВС, АМС, равны, то треугольник АВС равносторонний. Докажите это.

678. 2m-значное число назовём справедливым, если его чётные разряды содержат столько же чётных цифр, сколько и нечётные. Докажите, что в любом (2m + 1)-значном числе можно вычеркнуть одну из цифр так, чтобы полученное 2m-значное число было справедливым.

(Пример для числа 12345 показан на рисунке.)

679. а) На плоскости расположены четыре круга так, что первый касается второго в точке A, второй третьего — в точке B, третий четвёртого — в точке C, а четвёртый первого — в точке D. Докажите, что через четыре названные точки можно провести окружность или прямую.

б) В пространстве расположены четыре шара так, что первый касается второго в точке A, второй третьего — в точке В, третий четвёртого — в точке С, а четвёртый первого — в точке D. Докажите, что через четыре названные точки лежат в одной плоскости.

в) В пространстве расположены четыре шара так, что каждый касается трёх других. Докажите, что шесть точек касания принадлежат одной сфере или одной плоскости.

680. Два связиста играют в такую игру. Имеются n телефонных узлов, и связисты по очереди соединяют кабелем два из них по своему выбору. Выигрывает тот, после хода которого с любого узла можно будет дозвониться до любого другого (быть может, через несколько промежуточных; начало игры изображено на рисунке).

а) Выясните, кто выигрывает при n = 4, 5, 6, 7, 8 — начинающий или его партнёр?

в) Каков ответ при произвольном n?

в) Пусть игрок, связавший все узлы, проигрывает. Ответьте на вопросы пунктов а) и б) для этой новой игры.

г) Пусть вначале каждые два узла связаны кабелем, а связисты убирают по очереди по одному соединению. Игрок, нарушивший связность схемы, проигрывает. Вопрос тот же: кто выигрывает при правильной стратегии для n = 4, 5, 6, 7, 8? А для произвольного n?

Замечание. Можно было бы рассмотреть четвёртый вариант: считать, что в пункте г) игрок, нарушивший связность, выигрывает. Полное исследование этого варианта игры автору неизвестно.

681. а) Придумайте такие натуральные числа a, b, c и d, что числа a² + b², a² + b² + c² и a² + b² + c² + d² — квадраты целых чисел.

б) Существует ли такая последовательность, состоящая из квадратов натуральных чисел, что при любом n сумма n её первых членов — квадрат целого числа?

682. Внутри треугольника нужно расположить другой треугольник так, чтобы у каждого из трёх квадратов, построенных на сторонах внутреннего треугольника во внешнюю сторону, две вершины лежали на разных сторонах исходного треугольника.

а) Докажите, что медианы исходного треугольника перпендикулярны сторонам внутреннего треугольника.

б) Для любого ли исходного остроугольного треугольника такое построение возможно?

683. Несколько одинаковых кругов положили на стол так, что никакие два не перекрываются. Докажите, что круги можно раскрасить в четыре цвета так, что любые два касающихся круга будут окрашены в разные цвета. Нарисуйте расположение кругов, при котором трёх цветов для такой раскраски недостаточно.

684*. Двое играют в следующий вариант «морского боя». Один игрок располагает на доске n×n несколько непересекающихся «кораблей» n×1 (быть может, ни одного). Второй игрок наносит одновременно ряд ударов по полям доски и про каждое поле получает от противника ответ — попал или промахнулся. По какому минимальному числу полей следует нанести удары, чтобы по ответу противника можно было однозначно определить расположение всех его кораблей? Рассмотрите случаи, когда n равно а) 4; б) 10. в) А если n — любое натуральное число?

685*. Два подмножества множества натуральных чисел называют конгруэнтными, если одно получается из другого сдвигом на целое число. (Например, множества чётных и нечётных чисел конгруэнтны.) Можно ли разбить множество натуральных чисел на бесконечное число (не пересекающих друг друга) бесконечных конгруэнтных подмножеств?

686. Для любого ли числа x, удовлетворяющего неравенству x ³ 1, целая часть квадратного корня из целой части квадратного корня числа x равна целой части квадратного корня из квадратного корня числа x?

687. а) В девятиугольной пирамиде все 9 боковых рёбер и все 27 диагоналей основания окрашены: некоторые — в красный цвет, остальные — в синий. Докажите, что существуют три вершины пирамиды, служащие вершинами треугольника, все стороны которого одного цвета.

б) Верно ли аналогичное утверждение для восьмиугольной пирамиды?

688. Ни одно из натуральных чисел a₁, a₂, ..., a_n не превосходит своего номера; сумма всех их чётна. Докажите, что сумма нескольких из данных чисел равна сумме остальных данных чисел.

689*. Из равнобедренных трапеций с основаниями 3 см и высотой 1 см нельзя составить прямоугольник. Докажите это.

690*. а) Внутри выпуклого многоугольника с площадью S₁ и периметром P₁ расположен выпуклый многоугольник с площадью S₂ и периметром P₂. Докажите неравенство 2S₁P₂ > S₂P₁.

б) Сформулируйте и докажите аналогичное утверждение для выпуклых многогранников.

691. а) Найдите хотя бы одно такое k, что некоторое натуральное число можно представить как в виде произведения k последовательных чисел, бóльших 1, так и в виде произведения k + 2 таких чисел.

б) Никакое произведения двух последовательных натуральных чисел нельзя представить в виде произведения четырёх последовательных натуральных чисел. Докажите это.

692. Точки C₁, A₁ и B₁ так взяты на сторонах, соответственно, АВ, ВС и СА треугольника ABC, что

АС₁ : С₁В = ВA₁ : A₁С = CB₁ : BA₁ = 1 : 3.

Докажите, что периметр Р треугольника AВС и периметр Р₁ треугольника А₁В₁С₁ связаны неравенствами а) 4Р₁ < 3P; б) 2Р₁ > P.

693. В некотором посёлке 1000 жителей. Ежедневно каждый из них делится узнанными накануне новостями со всеми своими знакомыми. Любая новость становится известной всем жителям посёлка. Докажите, что можно выбрать 90 жителей так, что если одновременно всем им сообщить какую-то новость, то через 10 дней её будут знать все жители посёлка.

694. В каждой вершине куба записано число. За один шаг к двум числам, размещённым на одном (любом) ребре, прибавляют по единице. Можно ли за несколько таких шагов сделать все восемь чисел равными между собой, если вначале числа были поставлены, как на а) левом; б) среднем; в) правом рисунке?

695*. Можно ли все клетки какой-нибудь прямоугольной таблицы окрасить в белый и чёрный цвета так, чтобы чёрных и белых клеток было поровну, а в каждой строке и в каждом столбце было более ³⁄₄ клеток одного цвета?

696. Можно ли таблицу 10×10 клеток заполнить различными натуральными числами так, чтобы для любого квадрата k×k клеток, где 2 £ k £ 10, а) суммы; б) произведения k чисел на его диагоналях были одинаковы?

697. Назовём пузатостью прямоугольника отношение его меньшей стороны к большей (пузатость квадрата равна 1). Докажите, что, как бы ни разрезать квадрат на прямоугольники, сумма их пузатостей будет не меньше 1.

698. На сторонах a, b, c и d вписанного в окружность четырёхугольника «наружу» построены прямоугольники размерами a×c, b×d, c×a и d×b. Докажите, что центры этих прямоугольников являются вершинами а) параллелограмма; б) прямоугольника.

699. Полукруг с диаметром АВ разрезан отрезком СD, перпендикулярным АВ, на два криволинейных треугольника АСD и ВСD, в которые вписаны окружности, касающиеся АВ в точках Е и F. Докажите, что а) AD = AF; б) DF — биссектриса угла BDC; в) величина угла ЕDF не зависит от выбора точки С на АВ.

700. Можно ли множество всех конечных десятичных дробей разбить на а) два; б) три класса так, чтобы ни в один из классов не попали два числа, разность которых — степень числа 10, то есть число вида 10ⁿ, где n — целое?

701. Люда, Марина и Наташа нарисовали остроугольный треугольник LMN. Затем Люда построила свой треугольник, у которого длины двух сторон равны LM и LN, а величина угла между ними на 60° больше величины угла L треугольника LMN. Аналогично Марина построила свой треугольник со сторонами длинами ML и MN, величина угла между которыми на 60° больше величины угла M, а Наташа — свой, у которого величина угла между сторонами длин NL и NM на 60° больше величины угла N. Докажите, что третьи (новые) стороны трёх построенных треугольников одинаковы.

702. Обозначим через S_n сумму первых n простых чисел: S₁ = 2, S₂ = 2 + 3 = 5, S₃ = 2 + 3 + 5 = 10, S₄ = S₃ + 7 = 17 и так далее. Докажите, что для любого натурального n между S_n и S_n+1 есть хотя бы один точный квадрат.

703*. Решите систему уравнений 3(x + ¹⁄_x) = 4(y + ¹⁄_y) = 5(z + ¹⁄_z),   xy + yz + zx = 1.

704*. Вокруг квадрата описан параллелограмм (вершины квадрата лежат на разных сторонах параллелограмма). Докажите, что перпендикуляры, опущенные из вершин параллелограмма на стороны квадрата, тоже являются вершинами квадрата.

705. На прямоугольном листе клетчатой бумаги расположено несколько прямоугольных карточек, стороны которых лежат на линиях сетки. Карточки покрывают лист в два слоя (то есть каждую клетку листа покрывают в точности две карточки). Передвигать карточки нельзя.

а) Пусть карточки имеет размеры 1×2 клетки. Докажите, что можно выбрать часть карточек так, чтобы они покрыли лист в один слой.

Останется ли это верным, если карточки б) произвольных размеров; в*) размера 1×3 клетки?

706. Из центра каждой из двух данных окружностей проведены касательные к другой окружности. Докажите, что длины хорд, соединяющих точки пересечения касательных с окружностями (на рисунке эти хорды показаны красным цветом), равны.

707. Каждый из учеников класса занимается не более чем в двух кружках, причём для любой пары учеников существует кружок, в котором они занимаются вместе. Докажите, что найдётся кружок, где занимаются не менее ²⁄₃ учеников этого класса.

708. На сторонах выпуклого четырёхугольника площади S вне него построены квадраты, центры которых служат вершинами нового четырёхугольника площади S₁.

а) Докажите неравенство S₁ ³ 2S.

б) Докажите, что S₁ = 2S тогда и только тогда, когда диагонали исходного четырёхугольника равны по длине и взаимно перпендикулярны.

709*. Пол комнаты, имеющей форму правильного шестиугольника со стороной 10, заполнен плитками, имеющими форму ромба со стороной 1 и острым углом 60°. Разрешено вынуть три плитки, составляющие правильный шестиугольник со стороной 1, и заменить их расположение другим, как показано на рисунке. Докажите, что

а) из любого расположения плиток такими операциями можно получить любое другое;

б) это можно сделать не более чем за 1000 операций;

в) из расположения плиток нижнего левого рисунка нельзя получить расположение рисунка нижнего правого менее чем за 1000 операций.

710*. Существует ли такая возрастающая последовательность натуральных чисел, ни один из членов которой не равен сумме нескольких остальных, что n-й член этой последовательности для любого натурального числа n не превосходит числа а) 2 · 3^n/2; б) 10 · 1,5ⁿ; в) n¹⁰; г) 1000 · n^7/2; д) 1000 · n^3/2?

711. Диагонали выпуклого четырёхугольника ABCD, вписанного в окружность с центром O, взаимно перпендикулярны. Докажите, что ломаная АОС делит четырёхугольник на две части равной площади.

712. Любое положительное число можно представить в виде суммы девяти чисел, десятичные записи которых содержат только цифры 0 и до 7. Докажите это.

713. М — множество точек на плоскости. Точку О плоскости называем «почти центром симметрии» множества М, если из М можно выбросить одну точку так, что для оставшегося множества точка О является центром симметрии. Сколько «почти центров симметрии» может иметь конечное множество?

714*. N друзей одновременно узнали 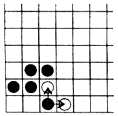N новостей, причём каждый узнал одну новость. Они стали звонить друг другу и обмениваться новостями. За один разговор можно передать сколько угодно новостей. Какое минимальное количество звонков необходимо, чтобы все узнали все новости? Рассмотрите три случая: а) N = 64; б) N = 55; в) N = 100.

715*. Прямой угол разбит на одинаковые клетки. На некоторых клетках стоят фишки, причём расположение фишек можно преобразовывать так: если для некоторой фишки соседняя сверху и соседняя справа клетки свободны, то в эти клетки ставим по фишке, а старую фишку убираем. Вначале в угловую клетку ставим одну лишь фишку. Можно ли указанными операциями освободить от фишек уголки из а) трёх; б) шести; в) десяти клеток, показанные на рисунках?

716. Из точки P внутри данного треугольника АВС опущены перпендикуляры PA₁, PB₁ и PC₁ на прямые ВС, АС и АВ. Для каких точек P внутри треугольника АВС сумма отношений BC/PA₁, CA/PB₁ и AB/PC₁ принимает наименьшее значение?

717. Рассмотрим всевозможные подмножества множества {1, 2, ..., n}, состоящие из r чисел, и в каждом выберем наименьшее число. Докажите, что среднее арифметическое всех выбранных чисел равно (n + 1) / (r + 1). Например, при n = 3 и r = 2 получаем три подмножества {1, 2}, {1, 3}, {2, 3}, и среднее арифметическое равно (1 + 1 + 2) / 3 = ⁴⁄₃.

718. Найдите наибольшее значение выражения вида m² + n² для таких всевозможных пар (m; n) натуральных чисел, что m £ 1981, n £ 1981 и ½n² – mn – m²½ = 1.

719. а) Для каких n ³ З существует множество из n последовательных натуральных чисел, обладающих следующим свойством: наибольшее из этих n чисел является делителем наименьшего общего кратного остальных n – 1 чисел?
б) При каких n ³ З существует единственное множество из n последовательных чисел, обладающих указанным свойством?

720. Функция f определена на множестве всех пар неотрицательных целых чисел (x; y) и для любых неотрицательных целых x и y удовлетворяет равенствам

• f (0; y) = y + 1,
• f (x + 1; 0) = f (x; 1),
• f (x + 1; y + 1) = f (x; f (x + 1; y)).

Вычислите f (4; 1981).