721. Каждая сторона треугольника поделена на три равные части. Точки деления служат вершинами двух треугольников, пересечение которых — шестиугольник. Найдите отношение площади этого шестиугольника к площади исходного треугольника.

722. В вершинах n-угольника расставлены в некотором порядке первые n натуральных чисел.

а) Докажите, что сумма n модулей разностей соседних чисел не меньше 2n – 2.

б) Для какого количества расстановок эта сумма равна 2n – 2?

723*. Существует ли такое бесконечное множество натуральных чисел, что ни одно из чисел этого множества и никакая сумма нескольких из них не является степенью натурального числа (a^k, где a и k — натуральные числа, k > 1)?

724. По плоскости ползут несколько черепах, скорости которых равны по величине, но различны по направлению. Докажите, что как бы черепахи ни были расположены вначале, через некоторое время они окажутся в вершинах выпуклого многоугольника.

725*. Пусть q_n — сумма n-х степеней косинусов углов величиной 180°/7, 540°/7 и 900°/7. Найдите а) q₁ и q₂; б) q₃ и q₄. в) Докажите, что q_n — рациональное число при любом натуральном n.

726. Точку внутри правильного 2n-угольника соединили с вершинами. Возникшие 2n треугольников раскрасили попеременно в голубой и красный цвет. Докажите, что сумма площадей голубых треугольников равна сумме площадей красных для а) n = 4; б) n = 3; в) любого натурального n.

727. Докажите неравенство a² + b² + c² + 2abc < 2, где a, b, c — длины сторон треугольника периметра 2.

728. Пусть А, В, С — вершины параллелепипеда, соседние с его вершиной P, а Q — вершина, противоположная Р. Докажите, что

а) расстояния от точек А, В и С до прямой РQ являются длинами сторон некоторого треугольника;

б) площадь S этого треугольника, объём V параллелепипеда и длина d его диагонали PQ связаны соотношением V = 2dS.

729. Найдите натуральное число, обладающее свойством: если записать рядом его квадрат и его куб, а затем переставить написанные цифры в обратном порядке, получится шестая степень этого числа.

730*. Последовательность a₁, a₂, a₃,... определена условиями a₁ = 0 и a_2n+1 = a_2n = n – a_n для любого натурального n. Например, a₁₀ = 5 – a₅ = 5 – (2 – a₂) = 3 + (1 – a₁) = 4:

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
an	0	1	1	1	1	2	2	3	3	4	4	4	4	5	5	5	5	6	6	6

а) Найдите a₁₉₈₂.

б) Каждое натуральное число входит в последовательность 2 или 4 раза. Докажите это. Сколько раз встретится в последовательности число 2k (при каждом натуральном k)?

в) Разность a_n – a_n–1 равна 1, если в разложение числа n на простые множители число 2 входит в нечётной степени, и 0 — в противном случае. Докажите это.

г) a_n = ⁿ⁄₃ для бесконечного множества значений n. Докажите это.

д) Найдётся ли n такое, что разность ½a_n – ⁿ⁄₃½ больше 1982?

е) Частное от деления a_n на n стремится к ¹⁄₃ при стремлении n к бесконечности. Докажите это.

731. Двое играют в такую игру: первый называет натуральное число от 2 до 9; второй умножает это число на произвольное натуральное число от 2 до 9; затем первый умножает результат на любое натуральное число от 2 до 9 и так далее; выигрывает тот, кто первым получит произведение больше а) тысячи; б) миллиона. Кто выигрывает при правильной игре — начинающий или его партнёр?

732. а) В треугольник ABC вписаны два разных прямоугольника так, что на основании AC лежат по две вершины каждого прямоугольника (а на сторонах AB и BC — по одной). Периметр каждого из прямоугольников равен 10. Найдите площадь треугольника ABC и докажите, что периметр любого вписанного в треугольник ABC прямоугольника, две вершины которого лежат на AC, тоже равен 10.

б) В четырёхугольник ABCD вписаны два прямоугольника с параллельными сторонами (так, что на каждой из сторон AB, BC, CD и DA лежит по одной вершине каждого прямоугольника). Периметр каждого из прямоугольников равен 10. Найдите площадь четырёхугольника ABCD и докажите, что для любой точки на любой из сторон четырёхугольника ABCD можно построить вписанный прямоугольник с вершиной в этой точке, стороны которого параллельны сторонам данного прямоугольникa и периметр которого также равен 10.

733. а) При каких натуральных m число 31^m – 1 делится на 2^m?

б*) Для любого нечётного а и натурального m существует бесконечно много таких натуральных k, что a^k – 1 делится на 2^m. Докажите это.

в*) Для любого нечётного а существует лишь конечное число таких натуральных m, что a^k – 1 делится на 2^m. Докажите это.

734. Биссектриса угла А треугольника ABC пересекает описанную окружность в точке K. Докажите, что длина проекции отрезка AK на прямую AB равна полусумме длин сторон AB и AC.

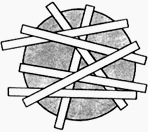735*. а) Круг диаметром 1 нельзя покрыть несколькими бумажными полосами, сумма ширин которых меньше 1. Докажите это.

б) Назовём слоем толщины h часть пространства, заключённого между параллельными плоскостями, находящимися на расстоянии h друг от друга. Докажите, что шар диаметром 1 нельзя покрыть несколькими слоями, сумма толщин которых меньше 1.

736. Медиана ВK и биссектриса СL треугольника АВС пересекаются в точке Р. Докажите равенство

PC · BC – AC · PL = PL · BC.

737. Обозначим через d_k количество тех домов некоторого города, в которых живёт не меньше k жителей, а через c_m — количество жителей в m-м по величине населения доме. Докажите равенства
а) c₁ + c₂ + c₃ + ... = d₁ + d₂ + d₃ + ...;
б) c₁² + c₂² + c₃² + ... = d₁ + 3d₂ + 5d₃ + ... + (2k – 1)d_k + ...;
в) d₁² + d₂² + d₃² + ... = c₁ + 3c₂ + 5c₃ + ... + (2k – 1)c_k + ...

738*. а) Количество прямых различных направлений, на которые данный n-угольник даёт одинаковые по величине проекции, не превосходит 2n;

б) максимальное число таких прямых для любого многоугольника чётно;

в) для треугольника это число больше трёх тогда и только тогда, когда треугольник остроугольный.

Докажите эти утверждения.

739. а) При любом значении х, для которого левая часть равенства имеет смысл, докажите равенство tg x + tg (x + 60°) + tg (x + 120°) = 3tg x · tg (x + 60°) · tg (x + 120°).

б) Для любого нечётного натурального числа n существует такое число c_n, что для любого числа x, для которого все нижеупомянутые тангенсы существуют, сумма тангенсов чисел вида x + ^πk⁄_n, где 0 £ k < n, равна произведению числа c_n на произведение этих тангенсов.

в*) Для каждого нечётного натурального числа n вычислите c_n.

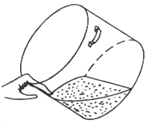740. Серёжа насыпал в цилиндрическую кастрюлю немного пшена и спросил соседку тетю Люду:
— Сколько нужно налить воды, чтобы получилась вкусная каша?
— Это очень просто,— ответила соседка. — Наклони кастрюлю — вот так; постучи, чтобы крупа пересыпалась и закрыла ровно половину дна. Теперь заметь точку на кастрюле, ближайшую к краю, до которой поднялась крупа — и зажми её пальцем! До этого уровня и надо налить воду.
— Так ведь пшена можно насыпать побольше и поменьше, да и кастрюли бывают разные — широкие и узкие,— усомнился Серёжа.
— Всё равно, мой способ годится в любом случае!— гордо ответила тетя Люда.

а) Докажите, что тетя Люда права: отношение объёмов воды и пшена по её рецепту всегда одно и то же.

б) Чему равно это отношение?

741. а) Найдите хотя бы одно натуральное число, которое делится на 30 и имеет ровно 30 различных делителей (включая 1 и само число).

б) Укажите все такие числа.

742. На а) окружности; б) сфере радиусом 1 расположены n точек. Докажите, что сумма квадратов расстояний между ними не превышает n².

743. В стране n городов.

а) Между любыми двумя городами имеется прямое сообщение самолетом или пароходом. Докажите, что, пользуясь лишь каким-то одним видом транспорта, из любого города можно попасть в любой другой (возможно, с пересадками).

б) Между любыми двумя городами имеется прямое сообщение самолетом, поездом или пароходом. Докажите, что можно выбрать не менее ⁿ⁄₂ городов и один из трёх видов транспорта так, что, пользуясь им одним, из любого выбранного города можно попасть в любой другой выбранный город.

в) Приведите пример, доказывающий, что в утверждении б) заменить число ⁿ⁄₂ бóльшим, вообще говоря, нельзя.

744*. В треугольник АВС вписан подобный ему треугольник А₁В₁С₁ (вершины А₁, В₁, С₁ углов, равных по величине углам А, B и C, лежат соответственно на отрезках ВС, СА и АВ). Пусть А₀, В₀, С₀ — точки пересечения прямых BВ₁ и CС₁, АA₁ и CС₁, BB₁ и AA₁. Докажите, что шесть окружностей, описанных около треугольников АВС₀, ВСA₀, АСB₀, А₁В₁С₀, A₁C₁B₀ и B₁C₁A₀, пересекаются в одной точке.

745. а) Ни одно из чисел d₁, d₂, d₃,... не превосходит по абсолютной величине числа 1. Докажите, что существует такая последовательность s₁, s₂, s₃,..., состоящая из чисел 1 и –1, что для всех натуральных n сумма чисел d₁s₁, d₂s₂, ..., d_ns_n по абсолютной величине не превосходит 1.

б) Для каждого натурального n задана тройка чисел (a_n, b_n, c_n), сумма которых a_n + b_n + c_n  равна нулю и ни одно из которых не превосходит по абсолютной величине числа 1. Построим новую последовательность троек (x_n, y_n, z_n), в которой x₀ = y₀ = z₀ = 0, а каждая очередная тройка (x_n, y_n, z_n) получается из предыдущей тройки (x_n–1, y_n–1, z_n–1) прибавлением к x_n–1 одного из чисел a_n, b_n и c_n по нашему выбору, к y_n-1 — другого, к z_n-1 — третьего. Можем ли мы всегда добиться того, что все числа x_n, y_n и z_n будут по абсолютной величине не больше 1 или хотя бы ограничены некоторой константой?

в) Ответьте на аналогичный вопрос для последовательностей четвёрок чисел.

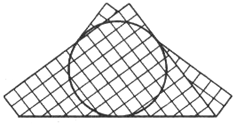746. Бумажный квадрат складываем пополам по некоторой прямой l, проходящей через его центр, в невыпуклый девятиугольник. Как нужно провести прямую l, чтобы:

а) площадь полученного девятиугольника была максимальной?

б*) в нём помещалась окружность наибольшего возможного радиуса?

747. а) Сумма n чисел равна 0, сумма их модулей равна a. Докажите, что разность между наибольшим и наименьшим из них не меньше 2a/n.

б*) Внутри выпуклого n-угольника А₁A₂A₃...A_n выбрана точка O так, что сумма векторов равна нулевому вектору, а сумма их длин равна d. Докажите, что периметр этого n-угольника не меньше 4d/n.

в*) Можно ли улучшить эту оценку (при некоторых n)?

748. а) Можно ли разместить на плоскости конечное число парабол так, чтобы их внутренние области покрыли всю плоскость?

Внутренней областью параболы мы называем выпуклую фигуру, границей которой служит эта парабола.

б*) В пространстве расположено несколько не пересекающих друг друга конусов. Докажите, что их нельзя переместить так, чтобы они покрыли всё пространство. (Конусом мы называем здесь неограниченную выпуклую фигуру, полученную в результате вращения некоторого угла вокруг его биссектрисы.)

749*. По кругу выписаны n положительных чисел. Вычислив частное от деления каждого из них на сумму двух соседних, сложим все частные. Докажите, что

а) при n = 3 сумма не меньше ³⁄₂ (и выясните, когда неравенство обращается в равенство);

б) при n > 3 сумма не меньше 2, причём равенство возможно только при n = 4;

в) при n > 4 число 2 нельзя заменить ни на какое большее число.

750. Докажите, что как бы ни раскрасить клетки бесконечного листа клетчатой бумаги в N цветов, найдутся

а) прямоугольник, вершины которого лежат в центрах клеток одного цвета, а стороны идут параллельно линиям сетки — по горизонтальным и вертикальным прямым;

б) l горизонтальных и m вертикальных прямых, которые пересекаются в центрах lm клеток одного цвета (l и m — любые натуральные числа);

в) равнобедренный прямоугольный треугольник, вершины которого — центры клеток одного цвета, при N = 2;

г*) то же для N = 3.

751*. На окружности намечены 3k точек, разделяющих её на 3k дуг, из которых k дуг имеют длину 1, ещё k дуг — длину 2, а остальные k дуг — длину 3. Докажите, что среди отмеченных точек есть две диаметрально противоположные.

752. Квадратная таблица n×n клеток заполнена целыми числами. При этом в клетках, имеющих общую сторону, записаны числа, отличающиеся друг от друга не больше, чем на 1. Докажите, что хотя бы одно число встречается в таблице не менее чем а) [ⁿ⁄₂]; б) n раз.

753. Числа a, b и c лежат на интервале (0, ^p⁄₂) и удовлетворяют равенствам: cos a = a, sin cos b = b и cos sin c = c. Расположите числа в порядке возрастания.

754*. а) Существуют ли такие многочлены P, Q и R от переменных x, y и z, что выполнено тождество

б) Тот же вопрос для тождества

755. Внутри тетраэдра выбрана некоторая точка. Докажите, что хотя бы одно ребро тетраэдра видно из неё под углом, косинус которого не больше числа –¹⁄₃.

756*. В стране, кроме столицы, больше 100 городов. Столица страны соединена авиалиниями со 100 городами; каждый из остальных городов соединён авиалиниями ровно с 10 городами. Из любого города можно (быть может, с пересадками) перелететь в любой другой. Докажите, что можно так закрыть половину авиалиний, идущих из столицы, что возможность попасть из любого города в любой сохранится.

757. Из последовательности 1, ¹⁄₂, ¹⁄₃, ¹⁄₄, ... легко выделить трёхчленную арифметическую прогрессию: ¹⁄₂, ¹⁄₃ и ¹⁄₆. Можно ли из этой последовательности выбрать арифметическую прогрессию длиной а) 4; б) 5; в) k, где k — любое натуральное число?

758*. Какое наименьшее количество чисел можно вычеркнуть из последовательности 1, 2, 3, ..., 1982, чтобы ни одно из оставшихся чисел не равнялось произведению двух других оставшихся чисел?

759. Внутри выпуклого четырёхугольника, у которого сумма всех шести расстояний между вершинами (то есть сумма длин всех сторон и диагоналей) равна S₁, расположен другой, для которого эта сумма равна S₂.

а) Может ли величина S₂ быть больше S₁?

б) Докажите неравенство 3S₂ < 4S₁.

в) Если внутри тетраэдра с суммой длин рёбер S₁ расположен другой, для которого эта сумма равна S₁, то 3S₂ < 4S₁. Докажите это.

760. С замкнутой ломаной A₁A₂...A_m, где m нечётно, проделываем такую операцию: середины её звеньев соединяем m отрезками через одну (середину A₁A₂ — с серединой A₃A₄, A₂A₃ — с A₄A₅, ..., A_{m – 1}A_m — с A₁A₂, A_mA₁ — с A₂A₃). С полученной ломаной вновь проделываем эту же операцию. Так же действуем и далее. Докажите, что из любой m-звенной ломаной при а) m = 5 — через 2 шага; б) m = 7 — через 3 шага; в*) любом нечётном m через некоторое (зависящее от m) число шагов получится ломаная, подобная (даже гомотетичная) первоначальной.

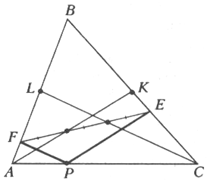761. Через произвольную точку Р стороны АС треугольника АВС параллельно его медианам АК и СL проведены прямые, пересекающие стороны ВС и АВ в точках Е и F соответственно. Докажите, что медианы АК и СL делят отрезок ЕF на три равные части.

762. Для любых положительных чисел a, b, c докажите неравенства

2abc(a + b + c) £ ab(a² + b²) + bc(b² + c²) + ca(c² + a²) £ 2(a⁴ + b⁴ + c⁴).

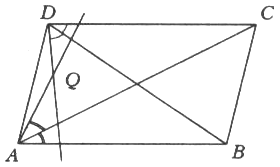763*. Дан параллелограмм ABCD, отличный от ромба. Прямая, симметричная прямой AB относительно диагонали AC, пересекает в точке Q прямую, симметричную прямой DC относительно диагонали DB. Найдите отношение QA : BD, если известно отношение QA : BD = k.

764. Уравнение а) x² + y³ = z⁵; б) x² + y³ + z⁵ = t⁷ имеет бесконечно много решений в натуральных числах. Докажите это.

765. Пусть В — конечное множество точек на плоскости, не лежащее на одной прямой.

а) Докажите, что найдутся три такие точки множества В, что проходящая через них окружность не содержит внутри себя других точек множества В.

б) Назовём триангуляцией множества В семейство треугольников с множеством вершин В, не налегающих друг на друга и в объединении дающих выпуклый многоугольник (триангуляцию множества В можно получить, соединяя его точки непересекающимися отрезками, пока это возможно). Докажите, что для любого В существует такая триангуляция, что окружность, описанная около любого треугольника этой триангуляции, не содержит внутри себя точек множества В. Укажите способ построения такой триангуляции.

в) Докажите, что если никакие четыре точки множества В не лежат на одной окружности, то описанная в пункте б) триангуляция единственна.

766. Сумма квадратов трёх последовательных целых чисел не может быть кубом натурального числа. Докажите это.

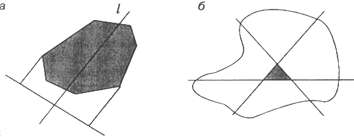767. Прямая делит площадь выпуклого многоугольника пополам. Докажите, что отношение, в котором эта прямая делит проекцию многоугольника на перпендикулярную к ней прямую, не превосходит суммы числа 1 и квадратного корня из 2.

б) Каждая из трёх прямых делит площадь данной фигуры пополам. Докажите, что площадь части фигуры, заключённой в треугольнике между тремя прямыми, не превосходит ¹⁄₄ всей площади фигуры.

768*. Сумма n чисел, ни одно из которых не превосходит по модулю 1, равна s. Докажите, что из них можно выбрать несколько чисел так, чтобы сумма выбранных чисел отличалась от ^s⁄₃ не более чем на ¹⁄₃.

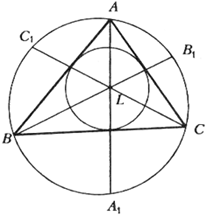769. Биссектрисы треугольника АВС пересекаются в точке L, их продолжения пересекают описанную окружность треугольника в точках X, Y, Z соответственно. Пусть R — радиус описанной, r — радиус вписанной окружности треугольника АВС. Докажите равенства

а) LX · LZ = R · LB;

б) LA · LC = r · LY;

в) S_ABC : S_XYZ = 2r : R.

770*. В основании треугольной пирамиды PABC лежит правильный треугольник АВС. Докажите, что если величины углов PAB, PBS, PCA равны, то пирамида PABC правильная.

771. В треугольнике АВС проведена биссектриса АК. Вписанная в треугольник АВК и описанная около треугольника АВС окружности концентричны. Найдите величины углов треугольника АВС.

772. В мастерской пять разных станков. Обучение одного рабочего работе на одном станке стоит 1000 рублей. С какими наименьшими затратами можно обучить 8 рабочих так, чтобы при отсутствии любых трёх из них все станки могли быть одновременно использованы в работе? Каждый рабочий может одновременно работать только на одном станке.

773. Вписанная в треугольник ABC окружность касается его сторон BC, CA и AB в точках X, Y и Z соответственно. Докажите, что если сумма векторов AX, BY и CZ равна нулю, то треугольник АВС равносторонний.

774*. Функция f (x), определённая на отрезке [0; 1], такова, что для любых чисел x и y отрезка [0; 1] значение функции в точке, являющейся полусуммой чисел x и y, не превосходит суммы значений функции f в точках x и y. Докажите, что

а) значения функции f во всех точках отрезка [0; 1] неотрицательны;

б) функция f равна нулю в бесконечном множестве точек отрезка [0; 1];

в) если существует такое число A, что значения функции f во всех точках отрезка [0; ¹⁄₂] не превосходят числа A, то и значения функции f во всех точках отрезка [0; 1] не превосходят числа A;

г*) если функция f непрерывна хотя бы в одной точке отрезка [0; 1], то она тождественно равна 0;

д*) существует функция f, удовлетворяющие условиям задачи и не во всех точках равная нулю.

775. Для каких натуральных n > 2 существуют такие различные натуральные числа a₁, a₂, ..., a_n, ни одно из которых не превосходит числа n + 1, что все n чисел ½a₁ – a₂½, ½a₂ – a₃½, ..., ½a_n–1 – a_n½, ½a_n – a₁½ различны?

776. На диагоналях AC и CE правильного шестиугольника ABCDEF взяты такие точки M и N соответственно, что AM : AC = CN : CE = λ. Найдите λ, если точки B, M и N лежат на одной прямой.

777. Дано уравнение x³ – xy² + y³ = n. Докажите, что

а) если натуральное n таково, что данное уравнение имеет целочисленное решение, то оно имеет по крайней мере три целочисленных решения;

б) при n = 2891 это уравнение не имеет целочисленных решений.

778*. A₁A₂A₃ — неравнобедренный треугольник; a_k — его сторона, лежащая против вершины A_k; M_k — середина этой стороны; T_k — точка её касания с окружностью, вписанной в данный треугольник; S_k — точка, симметричная T_k относительно биссектрисы угла A_k треугольника (k = 1, 2, 3). Докажите, что прямые M₁S₁, M₂S₂ и M₃S₃ имеют общую точку.

779*. Для невозрастающей последовательности положительных чисел, первый член которой равен 1, вычислим частное от деления квадрата каждого её члена на следующий член этой последовательности.

а) Докажите, что для любой исходной последовательности сумма некоторого набора таких частных не меньше 3,999.

б) Придумайте такую последовательность, что любая сумма таких частных меньше 4.

780*. Дан квадрат K со стороной 100. Пусть L такая — несамопересекающаяся незамкнутая ломаная, лежащая в K, что для любой точки Р границы квадрата K найдётся точка ломаной L, расстояние которой от Р не больше ¹⁄₂. Докажите, что на ломаной найдутся такие две точки X и Y, что расстояние между ними не превышает 1, а длина части заключённой между ними ломаной не меньше 198.