1666. Три плоскости разрезали куб с ребром 1 на 8 параллелепипедов. Докажите, что среди них есть хотя бы 4 параллелепипеда, объём любого из которых не превосходит ¹ ⁄ ₄.

1667. Натуральный ряд разбит на два бесконечных множества чисел. Докажите, что сумма некоторых 100 чисел одного из этих множеств равна сумме некоторых 100 чисел другого множества.

1668. Имеется n бочек, содержащих 1, 2, ..., n литров воды соответственно. Разрешено доливать в бочку столько воды, сколько в ней уже есть, из любой другой бочки, в которой воды достаточно для такой операции. Какое наибольшее количество воды можно собрать в одной бочке, если а) n = 10; б) n — любое натуральное число?

1669. Натуральные числа a, b и c таковы, что ab + bc = ca. Докажите равенства НОК[a,b] = НОК[b,c] = НОК[c,a].

1670. Диагонали AC и BD выпуклого четырёхугольника ABCD перпендикулярны. Серединные перпендикуляры к сторонам AB и CD пересекаются в точке P, лежащей внутри четырёхугольника. Докажите, что около ABCD можно описать окружность тогда и только тогда, когда площади треугольников ABP и CDP равны.

1671. На соревновании выступили a участников, их оценивали b судей, где b — нечётное число, не меньшее 3. За выступление каждого участника каждый судья ставил оценку «плюс» или «минус». Число k таково, что для любых двух судей существует не более k участников, получивших у них одинаковые оценки. Докажите неравенство 2bk ³ a(b – 1).

1672. Обозначим через τ(n) количество делителей числа n (включая 1 и n). Найдите все натуральные числа k, представимые в виде k = τ(n²) ⁄ τ(n).

1673*. Точка, расположенная внутри равностороннего треугольника, соединена отрезками с его вершинами. Из этой же точки опущены перпендикуляры на стороны треугольника. Шесть проведённых таким образом отрезков разделили треугольник на шесть прямоугольных треугольников. Покрасим их попеременно в красный и синий цвета. Докажите, что сумма радиусов окружностей, вписанных в красные треугольники, равна сумме радиусов окружностей, вписанных в синие треугольники.

1674. Функция f определена на множестве натуральных чисел. Сумма f (f (n)) + f (n) для любого чётного числа n равна 2n – 1, а для любого нечётного n она равна 2n + 1. Найдите f (1999).

1675*. Тетраэдр ABCD, где AB = CD = 2 и квадраты длин отрезков AC, BC, AD и BD равны 3, можно разрезать на а) 8; б) 27 подобных ему и конгруэнтных между собой тетраэдров. Докажите это.

1676. Отрезок AB разбит на чёрные и белые отрезки так, что сумма длин чёрных отрезков равна сумме длин белых отрезков. Для каждого чёрного отрезка вычисляем произведение его длины на расстояние от точки A до его середины и такие произведения складываем. Для каждого белого отрезка тоже вычисляем произведение его длины на расстояние от точки B до его середины и такие произведения складываем. Докажите, что «белая» и «чёрная» суммы равны.

1677. Диагонали параллелограмма ABCD пересекаются в точке O. Окружность, проходящая через точки A, B и O, касается прямой BC. Докажите, что окружность, проходящая через точки B, C и O, касается прямой CD.

1678. В таблице размером n×n в каждой строке и в каждом столбце в трёх клетках записаны какие-либо числа, остальные клетки пустые. При этом сумма чисел в каждой строке и в каждом столбце одна и та же. Для каждой строки перемножим её числа и полученные n произведений сложим. Аналогично, перемножим числа в каждом столбце и сложим полученные n произведений. Докажите, что «строчная» и «столбцовая» суммы равны.

1679. Последовательности a₀, a₁, a₂,... и b₀, b₁, b₂,... определим следующим образом. В качестве a₀ берём любое положительное число, а в качестве b₀ — любое отрицательное число. Для любого натурального числа n числа a_n и b_n — это, соответственно, положительный и отрицательный корень уравнения x² + a_n–1x + b_n–1. Найдите пределы обеих последовательностей.

1680*. Пусть C — натуральное число. Рассмотрим последовательность, n-й член которой равен n³ + C.

а) Докажите, что любые три подряд идущие члена последовательности не имеют общего делителя, отличного от 1.

б) Пусть С — куб натурального числа. Докажите, что существуют соседние члены последовательности, не являющиеся взаимно простыми числами.

в*) Существует ли такое натуральное число C, что любые соседние члены последовательности взаимно просты?

1681. Квадрат целого числа оканчивается так: ...21. Может ли третья справа цифра этого квадрата быть чётной?

1682. Из некоторой точки плоскости опущены перпендикуляры на высоты треугольника (или на их продолжения). Докажите, что основания перпендикуляров являются вершинами треугольника, подобного исходному.

1683. Имеется 20 бусинок десяти цветов, по две каждого цвета. Их как-то разложили в 10 коробок. Известно, что можно выбрать по бусинке из каждой коробки так, что все цвета будут представлены. Докажите, что количество способов такого выбора есть ненулевая степень двойки.

1684*. Круг разделён радиусами на 2n конгруэнтных секторов; n из них синие, остальные n — красные. В синие секторы, начиная с некоторого, по ходу часовой стрелки последовательно вписаны натуральные числа от 1<\nobr> до n. В красные секторы, начиная с некоторого, против хода часовой стрелки тоже числа вписаны числа от 1 до n. Докажите существование полукруга, в секторах которого — числа от 1 до n.

1685. В окружность вписан четырёхугольник ABCD. Докажите, проведённые через середины сторон треугольников ABC, BCD, CDA и DAB, имеют общую точку, а их центры лежат на одной окружности.

1686. Функции f и g непрерывны на отрезке [0; 1] и таковы, что интеграл от каждой из них по отрезку [0; 1] равен 1, а интеграл от функции, равной квадратному корню из суммы квадратов функций f и g, равен квадратному корню из числа 2. Докажите равенство функций f и g.

1687. Будем называть размером прямоугольного параллелепипеда сумму трёх его измерений — длины, ширины и высоты. Может ли в некотором прямоугольном параллелепипеде поместиться больший по размеру прямоугольный параллелепипед?

1688*. Рассмотрим функцию f (x) = (x² + ax + b) ⁄ (x² + cx + d), где трёхчлены x² + ax + b и x² + cx + d не имеют ни одного общего корня. Докажите равносильность следующих утверждений:

• существует интервал, свободный от значений функции f;
• функцию f можно представить в виде композиции линейных функций, возведения в квадрат и взятия обратного.

1689*. Рассмотрим произведение трёх натуральных чисел, образующих арифметическую прогрессию, являющееся делителем некоторого числа вида n² + 1, где n — натуральное число.

а) Докажите существование такой арифметической прогрессии с разностью 12.

б) Докажите несуществование такой прогрессии с разностью 10 или 11.

в*) Какое наибольшее число членов может содержать такая прогрессия с разностью 12?

1690. В каждой вершине выпуклого многогранника сходятся три ребра. Одна грань многогранника красная, остальные — синие, причём каждая синяя грань — вписанный многоугольник. Докажите, что и красная грань — вписанный многоугольник.

1691. Любой четырёхугольник можно разрезать на 3 трапеции. Докажите это.

1692. a, b и c — длины сторон треугольника. Докажите, что сумма чисел (a² + 2bc) ⁄ (b² + c²), (b² + 2ca) ⁄ (c² + a²) и (c² + 2ab) ⁄ (a² + b²) больше числа 3.

1693. Две окружности пересекаются в точках P и Q. Третья окружность с центром P пересекает первую в точках A и B, вторую — в точках C и D. Докажите равенство углов AQD и BQC.

1694. Парабола y = –x² + b₁x + c₁ и парабола y = –x² + b₂x + c₂ касаются параболы y = ax² + bx + c, где a > 0. Докажите, что прямая, проходящая через точки касания, параллельна общей касательной к первым двум параболам.

1695. Грани правильного тетраэдра окрасили в шахматном порядке. Докажите, что для любой внутренней точки сумма расстояний до плоскостей чёрных граней равна сумма расстояний до плоскостей белых граней.

1696. Рёбра графа покрашены n красками так, что из каждой вершины выходит по одному ребру каждого цвета. Для любого цвета по рёбрам этого цвета можно добраться от любой вершины графа до любой другой. Докажите, что какие бы n – 1 разноцветных рёбер графа ни уничтожить, граф останется связным.

1697. Сумма цифр десятичной записи числа n равна 100, а сумма цифр десятичной записи числа 44n равна 800. Чему равна сумма цифр десятичной записи числа 3n?

1698. На сторонах AB, BC и CA расположены точки C', A' и B' соответственно. Докажите, что если длины отрезков AA', BB' и CC' не превосходят 1, то утроенный квадрат площади треугольника ABC не превосходит 1.

1699. Для любого натурального n удвоенная сумма дробных частей квадратных корней из первых n² натуральных чисел не превосходит n² – 1. Докажите это.

1700*. На числовой прямой отмечены точки с координатами 1, 2, 3, ..., 2n. Блоха начала прыгать из точки 1 и через 2n рыжков, побывав во всех отмеченных точках, возвратилась в точку 1. Сумма длин первых 2n – 1 прыжков равна n(2n – 1). Докажите, что длина последнего прыжка равна n.

1701. Если x > 0, y > 0 и x² + y³ ³ x³ + y⁴, то x³ + y³ £ 2. Докажите это.

1702*. В некоторой группе из 12 человек среди каждых 9 человек есть 5 попарно знакомых. Докажите, что среди этих людей есть 6 знакомых друг с другом.

1703. Если a^m + b^m + c^m = 0 и aⁿ + bⁿ + cⁿ = 0, где m и n — натуральные числа, то abc = 0. Докажите это.

1704. На бесконечной клетчатой доске в каждой клетке квадрата размером n×n стоит по одной фишке. Ход — перепрыгивание любой фишки через соседнюю по стороне фишку, непосредственно за которой расположена пустая клетка; при этом ту фишку, через которую фишка перепрыгнула, снимаем. Докажите, что позиция, в которой невозможен ни один ход, не может возникнуть ранее чем через [n²⁄ 3] ходов.

1705. Через точку внутри сферы проведены три взаимно перпендикулярные плоскости, делящие сферу на 8 сферических треугольников. Докажите, что если их раскрасить в шахматном порядке, то сумма площадей 4 сферических треугольников одного цвета окажется равна сумме площадей других 4 треугольников.

1706. AL и BM — биссектрисы треугольника ABC. Одна из точек пересечения описанных окружностей треугольников ACL и BCM лежит на отрезке AB. Докажите, что величина угла ACB равна 60°.

1707*. Квадрат клетчатой бумаги размером n×n разрезан на 2n прямоугольников. При этом каждый прямоугольник расположен либо целиком ниже, либо выше ступенчатой ломаной, разделяющей квадрат. Докажите, что некоторая клетка клетчатой бумаги является одним из названных прямоугольников.

1708. Играют двое. Они по очереди пишут на доске делители числа 100!, отличные от 1 (без повторений!). Проигрывает тот игрок, после хода которого числа на доске окажутся взаимно просты в совокупности. Кто выигрывает при правильной игре: начинающий или его противник?

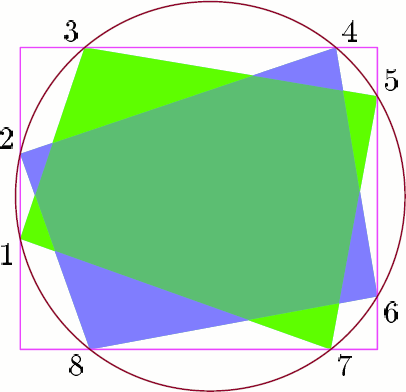1709. Окружность пересекает стороны прямоугольника в восьми точках, которые последовательно занумерованы. Докажите, что площадь четырёхугольника с вершинами в точках с нечётными номерами равна площади четырёхугольника с вершинами в точках с чётными номерами (другими словами, сумма площадей синих треугольников равна сумме площадей зелёных треугольников).

1710. Числа p, q, r, x, y, z положительные, причём p + q + r =1 и x^py^qz^r = 1. Докажите, что удвоенная сумма частных p²x² ⁄ (qy + rz), q²y² ⁄ (rz + px) и r²z² ⁄ (px + qy) не меньше 1.