1846. Для любого натурального n и любого натурального k £ n докажите неравенство (1 + ¹⁄_n)^k £ (n² + nk + k²) ⁄ n².

1847. В 8 банках сидят 80 пауков. Разрешено выбрать любые две банки, суммарное число пауков в которых чётное, и пересадить часть пауков из одной банки в другую, чтобы их стало поровну. При любом ли начальном распределении пауков в банках с помощью нескольких таких операций можно добиться того, чтобы в банках оказалось поровну пауков?

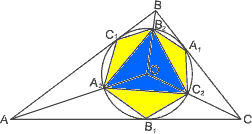1848. В треугольник АВС вписана окружность с центром О, которая касается сторон в точках А₁, В₁, С₁. Отрезки АО, ВО, СО пересекают окружность в точках А₂, В₂, С₂. Докажите, что площадь треугольника А₂В₂С₂ равна половине площади шестиугольника В₁А₂С₁В₂А₁С₂.

1849. Простое число p удовлетворяет равенству p² = 2ⁿ · 3^m + 1, где n и m — целые неотрицательные числа. Докажите неравенство p < 18.

1850. Числа натурального ряда от 1 до n(n + 1) записаны последовательно красным и синим цветами в следующей очерёдности. Первые n чисел — красные, затем одно — синее, затем (n – 1) чисел — красные, затем два — синие и так далее, наконец, одно число — красное, а последние n чисел — синие. Таким образом, убывающие по численности группы красных чисел перемежаются с возрастающими по численности группами синих чисел. Докажите, что сумма синих чисел вдвое больше суммы красных чисел.

1851. Нарисованы координатные оси Ох, Оу и график функции y = ¹⁄_8x. Масштаб не указан. Пользуясь только циркулем, постройте точку (1;1).

1852. Дано натуральное число n. В интервале (n²; n² + n) выбраны различные натуральные числа a и b. Докажите, что в этом интервале нет натуральных делителей числа ab, отличающихся от a и b.

1853. С числом разрешено делать следующее: возвести в любую натуральную степень или отрезать последние две цифры, умножить образованное ими число на 3 и прибавить к числу, образованному остальными цифрами. Можно ли с помощью таких операций из числа 81 получить число 82?

1854*. Пусть f (x) — многочлен степени m > 1 с целыми коэффициентами. Докажите, что множество значений многочлена f (x) в целых точках содержит бесконечную геометрическую прогрессию тогда и только тогда, когда f (x) = a(bx + c)^m, где a, b — ненулевые целые числа, c — целое число.

1855. Плоскости, параллельные граням прямоугольного параллелепипеда, разрезали его на меньшие параллелепипеды, которые окрасили в чёрный и белый цвета в шахматном порядке. Известно, что сумма объёмов чёрных параллелепипедов равна сумме объёмов белых. Докажите, что из чёрных параллелепипедов можно составить параллелепипед P, а из белых можно составить равный ему параллелепипед Q.

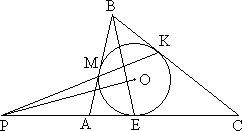1856. Окружность с центром О, вписанная в треугольник АВС, касается его основания АС в точке Е, а боковых сторон — в точках М и К. Прямая МК пересекает продолжение основания в точке Р. Докажите перпендикулярность прямых РО и ВЕ.

1857. На окружности находится множество К, состоящее из k точек, делящих окружность на k равных дуг. В К взяты два подмножества М и N, содержащие m и n точек соответственно. У подмножеств М и N ровно r общих точек. Более того, на какой бы угол, кратный ^2p⁄_k, мы ни повернули подмножество N, оно по-прежнему будет иметь ровно r общих точек с подмножеством М. Докажите равенство rk = mn.

1858. Даны такие натуральные числа a и b, что числа 2a + 1 и 2b + 1 взаимно просты. Каким может быть наибольший общий делитель чисел 2^2a+1 + 2^a+1 + 1 и 2^2b+1 + 2^b+1 + 1?

1859. Квадратный стол площади 2 можно в два слоя покрыть четырьмя квадратными салфетками, площадь каждой из которых равна 1. Более того, это можно сделать 100 различными способами. Найдите эти способы. (Салфетки можно перегибать, но нельзя разрывать.)

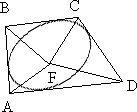1860. Точка F является одним из фокусов эллипса, вписанного в выпуклый четырёхугольник ABCD. Докажите, что сумма величин углов AFB и CFD равна 180°.

1861. Среди любых n + 1 вершин правильного (2n + 1)-угольника, где n > 1, найдутся три, являющиеся вершинами равнобедренного треугольника. Докажите это.

1862. Биссектрисы AD, BE и CF треугольника АВС пересекаются в точке I. Докажите, что треугольник АВС правильный, если а) ID = IF = IE; б) треугольник DFE правильный.

1863*. Рассмотрим последовательность, первые два члена которой равны 1 и 2 соответственно, а каждый следующий член — наименьшее натуральное число, которое ещё не встретилось в последовательности и которое не взаимно просто с предыдущим членом последовательности. Докажите, что каждое натуральное число входит в эту последовательность.

1864. В квадрат ABCD вписана ломаная MKALN так, что величины углов MKA, KAL и ALN равны 45°. Докажите равенство MK² + AL² = AK² + NL².

1865*. Для натурального числа n = 46 можно указать натуральное число m = 460100021743857360295716, обладающее следующими свойствами:

• первые цифры числа m представляют собой число n;
• если эти первые цифры перенести в конец числа m, то (отбросив при необходимости первые нули, получим число 10002174385736029571646, которое ровно в n раз меньше числа m.

Для каких ещё натуральных n существует число m, обладающее такими же свойствами?

1866. Остров разделён на княжества, каждое из которых представляет собой на карте острова параллелограмм. При этом любые два параллелограмма либо не имеют общего участка границы, либо в качестве общего участка границы имеют общую сторону. Докажите, что для правильной раскраски карты острова достаточно трёх красок. (Раскраска правильная, если любые два княжества, имеющие общий участок границы, закрашены в разные цвета.)

1867*. Пусть М — множество членов некоторой геометрической прогрессии. Каково наибольшее возможное число элементов в пересечении множества М с множеством чисел вида а) 2ⁿ – 1, где n — целое; б) 2ⁿ + 1, где n — целое?

1868. Рассмотрим множество всех квадратных таблиц размером p×p, где p > 1, заполненных натуральными числами 1, 2, …, р². Назовём правильной таблицу, в которой в первой строке стоят по порядку числа 1, 2, …, р, во второй строке — (р + 1), р + 2, …, 2р, и так далее. Пусть А — подмножество множества таблиц,в котором каждую таблицу можно получить из правильной операциями перестановки столбцов и перестановки строк, В — подмножество, в котором операциями прибавления числа 1 ко всем числам строки или столбца из любой таблицы можно получить таблицу с равными числами. Докажите, что А = В тогда и только тогда, когда р — простое.

1869. а) Решите уравнение sin⁸x + ¹⁄_sin⁸x = cos⁸x + ¹⁄_cos⁸x.

б) Пусть x и y — положительные числа, не равные друг другу и удовлетворяющие равенству xⁿ + ¹⁄_xⁿ = y^m + ¹⁄_y^m, где m и n — натуральные числа. Докажите неравенство x² + y² > (¹⁶⁄₉)^{1/(m + n)}.

1870. а) На плоскости даны точки A, B, C и D общего положения (то есть никакие три из них не лежат на одной прямой). Известно. что углы между прямыми АВ и CD, AC и BD, AD и ВС равны. Докажите, что они прямые.

б) Углы между противоположными рёбрами тетраэдра равны. Верно ли, что они прямые?

1871. За круглым столом 35 гостей уселись пить чай. Им выдали 10 литровых и 25 пол-литровых кружек. Каждому принесли пол-литровый чайник с чаем. Гость может вылить содержимое чайника себе или одному из своих соседей. Гости согласны пить только из полной кружки. Какое наибольшее число гостей могут выпить?

1872. Прямоугольник разрезан на прямоугольники, у каждого из которых хотя бы одна сторона принадлежит границе исходного прямоугольника. Докажите, что найдутся два прямоугольника с общей стороной.

1873. В стране несколько городов, соединённых дорогами с односторонним и двусторонним движением. Из любого города в любой другой можно проехать ровно одним путём, не проходящим два раза ни через какой город. Докажите, что города можно распределить между тремя губерниями так, чтобы любая дорога соединяла города из разных губерний.

1874. Решите уравнение х^у – у^х = 1 в натуральных числах х и у.

1875. Сколько может быть граней у выпуклого многогранника, для любого ребра которого соответствующий внутренний двугранный угол острый?

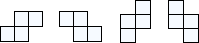1876. а) Во всех клетках квадрата n×n стоят минусы. За один ход можно поменять знаки в одной из изображённых четырёх фигурок. При каких n можно получить плюсы во всех клетках квадрата?

б) Докажите, что если в каком-то квадрате поменяли таким образом все знаки, то при этом фигурки каждого из четырёх видов использовались одинаковое по чётности число раз.

1877. За 64 хода король обошёл все поля шахматной доски и вернулся на прежнее место. Среди прочих он сделал ходы a2-b2 и g8-g7. Докажите, что король сделал не меньше двух диагональных ходов.

1878. На высоте CH треугольника ABC построена, как на диаметре, окружность. Докажите, что касательные к этой окружности, проведённые в точках её пересечения со сторонами АС и ВС, пересекаются на медиане СМ треугольника.

1879. На левую и правую чашки весов положили по 100 гирек из набора 1 г, 2 г, 3 г, ..., 200 г. Значимостью гирьки с какой-либо чашки назовём количество гирек с другой чашки, которые легче её. Докажите, что весы покажут равновесие тогда и только тогда, когда сумма значимостей гирек левой чашки равна сумме значимостей гирек правой чашки.

1880. На прямой даны 2k – 1 белых и 2k – 1 чёрных отрезков. Известно, что любой белый отрезок пересекается хотя бы с k чёрными, а любой чёрный — хотя бы с k белыми. Докажите, что хотя бы один из чёрных отрезков пересекается со всеми белыми отрезками, и хотя бы один белый отрезок пересекается со всеми чёрными.

1881. Пусть a, b, c — положительные числа, сумма которых равна 1. Докажите, что половина суммы обратных величин чисел (1 – a), (1 – b) и (1 – c) не меньше суммы обратных величин чисел (1 + a), (1 + b) и (1 + c).

1882. Изначально у Ани и Бори было по длинной полосе бумаги. На одной из них была написана буква А, а на другой — Б. Каждую минуту один из них (не обязательно по очереди) приписывает к слову на своей бумажке слово с бумажки другого. Докажите, что через сутки слово с полоски Ани можно будет разрезать на две части и переставить их местами так, что получится то же слово задом наперёд.

1883. Решите в целых числах уравнение а) x⁴ – 2y² = 1; б) x² – 2y⁴ = 1; в) x⁴ – 8y² = 1; г) x⁴ – 8y² = 1.

1884. а) Квадрат разрезан на квадраты, один из которых красный, а остальные синие. Периметр каждого синего квадрата является целым числом. Докажите, что периметр красного квадрата — тоже целое число.

б) Равносторонний треугольник разрезан на равносторонние треугольники, один из которых красный, а остальные синие. Периметр каждого синего треугольника является целым числом. Докажите, что периметр красного треугольника — целое число.

1885. Автомобильная стоянка представляет собой ряд из n мест, занумерованных слева направо числами от 1 до n, а въезд на стоянку находится справа. У въезда скопились n машин, и теперь они по очереди заезжают на стоянку. Каждый водитель сначала подъезжает к своему любимому месту. Если оно свободно, ставит туда машину, а если занято, то едет вперёд до ближайшего свободного места (назад поворачивать нельзя). Обозначим a_k, где k £ n, номер любимого места водителя k-й в очереди машины. Будем говорить, что последовательность a₁, a₂, ..., a_n бесконфликтна, если удаётся поставить машины на стоянку, соблюдая указанные выше правила. Например, при n = 2 последовательности (1, 2), (2, 1) и (2, 2) бесконфликтны, а последовательность (1, 1) конфликтна.

а) Докажите, что последовательность натуральных чисел a₁, a₂, ..., a_n бесконфликтна тогда и только тогда, когда ни один её член не превосходит n и когда для любого натурального k, где k < n, количество членов последовательности, не превосходящих k, не превосходит k. Найдите количество б*) бесконфликтных последовательностей длины n; в*) бесконфликтных неубывающих последовательностей длины n.

1886. На столе лежат картинками вниз 8 игральных карт. Вы можете указать на любую группу карт (в частности, на одну карту или, например, на все 8) и спросить, сколько карт бубновой масти в этой группе. В качестве ответа вам сообщат число, отличающееся от истинного значения на 1. Научитесь при помощи 5 вопросов узнавать количество бубновых карт, лежащих на столе.

1887. Из точки пересечения диагоналей описанного четырёхугольника опущены перпендикуляры на его стороны. Докажите, что сумма величин, обратных длинам перпендикуляров, опущенных на некоторые две противоположные стороны, равна сумме величин, обратных длинам других двух перпендикуляров.

1888. В шкатулке лежат n монет достоинством в целое число дукатов каждая на сумму 2n – 1 дукатов. Докажите, что любую сумму от 1 до 2n – 1 можно выплатить монетами из шкатулки.

1889. На плоскости даны точки A₁, A₂, …, А_n и точки B₁, B₂, …, B_n. Докажите, что точки B₁, B₂, …, B_n можно перенумеровать так, чтобы для любой пары разных индексов i и j угол между векторами А_iA_j и В_iВ_j был острым или прямым.

1890. Четыре хорды разделили круг на девять частей, одна из которых (зелёная на рисунке) — прямоугольник. Площадь этого (зелёного) прямоугольника и площади ещё семи (синих) частей — рациональные числа. Докажите, что площадь (красного) криволинейного треугольника — рациональное число.